Простые дроби

Рассмотрим сначала простейшие рациональные функции – так называемые простые (или элементарные) дроби:

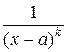I. , II. ,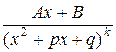

где . Предполагается, что квадратный трехчлен 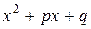не имеет действительных корней, т.е. .

Дробь вида I легко интегрируется. Действительно, пр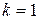и и 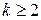получим

;

.

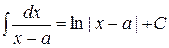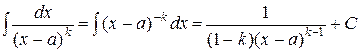Для интегрирования дроби вида II выделим из выражения 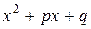полный квадрат:

.

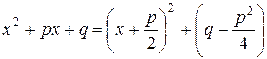Так как , то 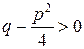, и, следовательно, число 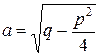является вещественным. Положим 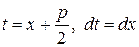. Тогда

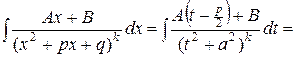
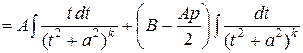. (8)

В случае 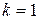каждый из полученных интегралов легко вычисляется подстановко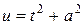й и 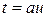соответственно:

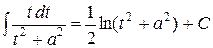и .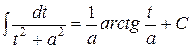

В случае 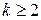для первого интеграла в правой части равенства (8) вновь применим подстановку :

;

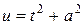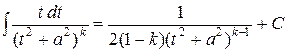что касается второго интеграла, то замена 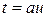сводит его к интегралу типа (6) и, следовательно, для его вычисления можно воспользоваться рекуррентной формулой (7).