 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства неопределенных интегралов
|
|
Теорема 3. Имеют место равенства
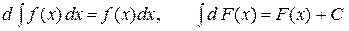 , (1)
, (1)
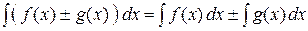 , (2)
, (2)
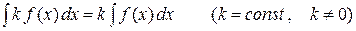 . (3)
. (3)
 Равенства (1) непосредственно следуют из определения. Равенства (2) и (3) устанавливаются однотипными рассуждениями, поэтому ограничимся доказательством равенства (3). Пусть
Равенства (1) непосредственно следуют из определения. Равенства (2) и (3) устанавливаются однотипными рассуждениями, поэтому ограничимся доказательством равенства (3). Пусть 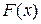 – первообразная для
– первообразная для  , тогда
, тогда 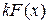 – первообразная для
– первообразная для 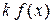 . Следовательно,
. Следовательно,
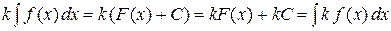 .
.
Здесь использован тот факт, что если 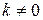 , то выражение
, то выражение 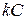 так же, как и само
так же, как и само 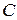 , означает произвольную постоянную. ▲
, означает произвольную постоянную. ▲
Из приведенных в теореме 3 свойств неопределенных интегралов особо отметим равенства (1), означающие, что знаки 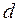 и
и 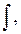 стоящие рядом, взаимно уничтожаются. Это легко объяснимо, если вспомнить, что дифференцирование и интегрирование – взаимно обратные операции.
стоящие рядом, взаимно уничтожаются. Это легко объяснимо, если вспомнить, что дифференцирование и интегрирование – взаимно обратные операции.
4. Таблица основных интегралов. Пользуясь таблицей производных основных элементарных функций, несложно составить аналогичную таблицу неопределенных интегралов.
Таблица
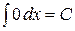
| 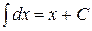
|
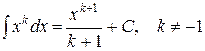
| 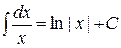
|
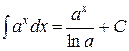
| 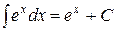
|
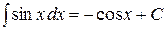
| 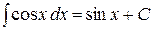
|
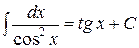
| 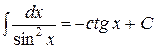
|
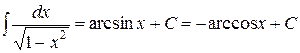
| 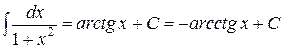
|
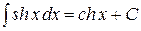
| 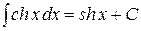
|
5. Основные методы интегрирования. При вычислении производных обычно пользуются стандартным набором правил и формул, что превращает дифференцирование в единообразную, выполняемую по одним и тем же схемам, работу. Иначе обстоит дело с интегрированием функций. Не существует единого рецепта вычисления неопределенного интеграла, пригодного для произвольных элементарных функций. Поэтому приходится рассматривать отдельные классы функций и для них разрабатывать правила по вычислению интегралов.
а) Непосредственное интегрирование
Вычисление интегралов с помощью непосредственного использования таблицы основных интегралов и свойств неопределенных интегралов называют непосредственным интегрированием.
Пример. Вычислить: 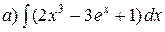 ;
; 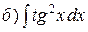 .
.
б) Метод замены переменной
Одним из основных при интегрировании функций является метод замены переменной (или метод подстановки), определяемый равенством
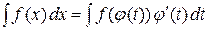 , (4)
, (4)
где 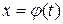 – дифференцируемая функция, определенная на некотором промежутке так, что существует сложная функция
– дифференцируемая функция, определенная на некотором промежутке так, что существует сложная функция 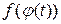 .
.
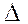 Для доказательства формулы (4) заметим, что по правилу дифференцирования сложной функции при
Для доказательства формулы (4) заметим, что по правилу дифференцирования сложной функции при 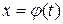 имеем
имеем
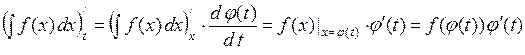 .
.
Это равенство означает, что при 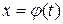 интеграл
интеграл 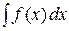 есть в то же время и неопределенный интеграл от функции
есть в то же время и неопределенный интеграл от функции 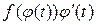 , т.е.
, т.е.
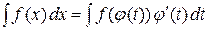 . ▲
. ▲
Формула (4) обычно применяется в тех случаях, когда непосредственное вычисление интеграла 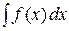 затруднительно, однако подстановкой
затруднительно, однако подстановкой 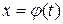 можно перейти к интегралу, более удобному для исследования.
можно перейти к интегралу, более удобному для исследования.
Одним из вариантов метода замены переменной является способ подведения под знак дифференциала, заключающийся в преобразовании:
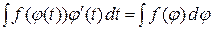 .
.
Примеры. 1) Вычислить 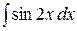 . Это не табличный интеграл (мешает число 2). Произведем замену
. Это не табличный интеграл (мешает число 2). Произведем замену 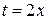 ; тогда
; тогда 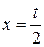 , и
, и 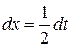 . Поэтому
. Поэтому
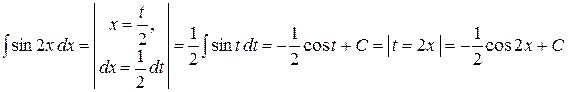 .
.
2) Вычислить 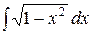 . Подынтегральная функция определена при
. Подынтегральная функция определена при 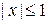 . Выполним замену
. Выполним замену 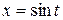 , где
, где 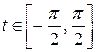 . Тогда
. Тогда 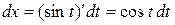 ,
, 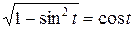 . Следовательно,
. Следовательно,
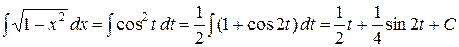 .
.
Возвращаясь к переменной 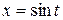 посредством равенства
посредством равенства 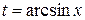 , получим:
, получим:
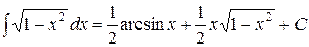 .
.
3) Вычислить 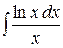 . Так как
. Так как 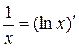 , то можно воспользоваться способом подведения под знак дифференциала. Имеем
, то можно воспользоваться способом подведения под знак дифференциала. Имеем
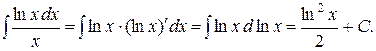
Общих рекомендаций по разыскиванию нужной подстановки не существует. Умение здесь создается упражнениями.
в) Метод интегрирования по частям
Дата публикования: 2015-09-17; Прочитано: 316 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
