Разложение правильных рациональных дробей на сумму простых

Рассмотрим теперь произвольную правильную дробь 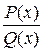. Ее интегрирование основано на теореме из алгебры, устанавливающей, что каждая правильная дробь может быть представлена в виде суммы конечного числа простых дробей.

Указанное представление тесным образом связано со следующим утверждением: любой многочлен 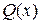с вещественными коэффициентами может быть представлен в виде произведения

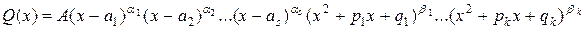, (9)

где , , а многочлены не имеют действительных корней. При этом, конечно, выполняется соотношение

.

Целые числа называются соответственно кратностями корней , а целые числа – кратности соответствующих комплексно сопряженных корней многочлена .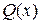

Приведем теперь без доказательства теорему о разложении правильной рациональной дроби на сумму простых, которая и позволяет интегрировать рациональные функции.

Теорема 4. Пусть 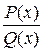– правильная рациональная дробь, а знаменатель 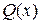разлагается на множители в виде (9). Тогда дробь 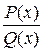можно единственным образом представить в виде суммы простых дробей:

, (10)

где , , 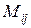– вещественные числа.

Замечание. Выражение в правой части разложения (10) выглядит так громоздко только из-за того, что оно выписано в максимальной общности. При решении конкретных примеров все обстоит значительно проще.

Равенство (10) выполняется для всех 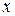, не являющихся вещественными корнями многочлена .

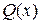Для того чтобы определить числа , , 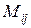, умножим обе части разложения (10) с неизвестными пок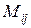а , , на 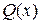. В результате умножения придем к равенству между многочленом 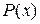и многочленом, который получится в правой части. Это означает, что коэффициенты, стоящие при равных степенях 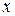, должны быть равны между собой. Приравнивая их, получим систему линейных уравнений, из которой определим неизвестные числа , , .

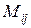Изложенный метод отыскания коэффициентов разложения рациональной функции называется методом неопределенных коэффициентов. После разложения дроби 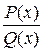на сумму простых дробей ее интегрирование сводится к сумме интегралов от простых дробей, приемы вычисления которых изложены выше.

Пример. Вычислить

.

Разложим дробь на сумму простых:

. (11)

Умножая обе части равенства (11) на знаменатель , имеем

, или

.

Приравнивая теперь коэффициенты при одинаковых степенях многочленов слева и справа в последнем равенстве, получаем систему линейных уравнений (относительно ):

Решая полученную систему (например, методом Гаусса), найдем

.

Вернемся к вычислению интеграла:

. ▲