Тригонометрические функции

а) Интегралы вида , .

Если 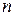– нечетное число, т.е. , то используют подстановку :

.

Мы получили интеграл от рациональной функции. Аналогично, если , то применяется подстановка .

Если и 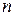четные числа (), то подынтегральное выражение преобразуют с помощью следующих формул понижения степени:

.

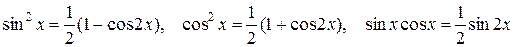Пример. Вычислить

.

. ▲

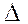
б) Интегралы вида ,

где – рациональная функция переменных .

Рациональной функцией переменных называют функцию вида

,

где и – многочлены двух переменных, т.е.

, .

Указанный интеграл может быть вычислен с помощью универсальной подстановки

.

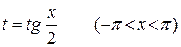Действительно, во-первых, и, следовательно, . Во-вторых, применяя известные формулы тригонометрии, получим

.

Тогда исходный интеграл преобразуется к виду

,

в котором подынтегральное выражение является рациональной функцией и, следовательно, интеграл может быть вычислен в соответствии с изложенной ранее схемой.

Пример. Вычислить .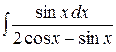

Применяя универсальную тригонометрическую подстановку, получим интеграл

,

для вычисления которого можно воспользоваться методом неопределенных коэффициентов. ▲

На практике универсальная подстановка часто приводит к громоздким выкладкам. В ряде случаев более удобны другие подстановки:

1) , если ;

2) , если ;

3) , если .

Пример. Вычислить

.

Здесь можно использовать универсальную подстановку, но поскольку , положим . Тогда

. ▲