 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Интегрирование некоторых классов функций 8
|
|
Составитель: кандидат физ.-мат. наук Подкуйко М.С.
СОДЕРЖАНИЕ
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 3
ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ КЛАССОВ ФУНКЦИЙ 8
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 17
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 26
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 32
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Основной задачей дифференциального исчисления является отыскание производной заданной функции. Здесь рассматривается обратная задача: восстановить функцию по известной производной. Указанная задача является основной для интегрального исчисления.
1. Первообразная. Символом  будет обозначаться промежуток на числовой оси
будет обозначаться промежуток на числовой оси 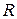 , т.е.
, т.е.  – это множество вида
– это множество вида  ,
,  ,
,  или
или  , причем промежуток может быть и бесконечным.
, причем промежуток может быть и бесконечным.
Определение. Функция 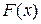 называется первообразной для функции
называется первообразной для функции  на промежутке
на промежутке  , если для
, если для  выполнено равенство
выполнено равенство  .
.
Например, для функции  первообразной на всей числовой оси служит функция
первообразной на всей числовой оси служит функция  , т.к.
, т.к.  . Отметим, что для функции
. Отметим, что для функции  первообразной будет и любая функция вида
первообразной будет и любая функция вида  , где
, где 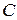 – произвольная постоянная. Этот факт носит общий характер. А именно, верна очевидная
– произвольная постоянная. Этот факт носит общий характер. А именно, верна очевидная
Теорема 1. Если 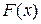 – первообразная для
– первообразная для  , то функция
, то функция  при любом значении постоянной
при любом значении постоянной 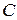 также является первообразной для
также является первообразной для  .
.
Таким образом, если функция  имеет первообразную
имеет первообразную 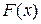 , то она имеет семейство первообразных вида
, то она имеет семейство первообразных вида  . Оказывается, кроме функций из этого семейства, других первообразных функция
. Оказывается, кроме функций из этого семейства, других первообразных функция  иметь не может. Для установления этого важного факта понадобится
иметь не может. Для установления этого важного факта понадобится
Лемма 1. Если  на промежутке
на промежутке  , то
, то  , где
, где 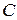 – некоторая постоянная.
– некоторая постоянная.
 Лемма будет доказана, если показать, что для
Лемма будет доказана, если показать, что для  выполнено равенство
выполнено равенство  . Пусть
. Пусть  ,
,  . По теореме Лагранжа
. По теореме Лагранжа  такое, что
такое, что  . Но так как
. Но так как  для
для  , то
, то  ; следовательно,
; следовательно,  . ▲
. ▲
Теорема 2. Если 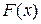 – первообразная для
– первообразная для  , то любая другая ее первообразная представляется в виде
, то любая другая ее первообразная представляется в виде  при некотором значении постоянной
при некотором значении постоянной 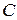 .
.
 Пусть
Пусть 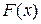 и
и  – две первообразные для
– две первообразные для  . Теорема будет доказана, если показать, что при некотором постоянном
. Теорема будет доказана, если показать, что при некотором постоянном 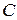 выполнено тождество
выполнено тождество  . Положим
. Положим  . Имеем
. Имеем
 .
.
Тогда в силу леммы 1  , т.е.
, т.е.  . ▲
. ▲
2. Понятие неопределенного интеграла. Пусть 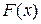 – некоторая первообразная для функции
– некоторая первообразная для функции  . Тогда в силу теоремы 2 множество всех ее первообразных – это семейство функций вида
. Тогда в силу теоремы 2 множество всех ее первообразных – это семейство функций вида  . Это семейство функций называют неопределенным интегралом (от) функции
. Это семейство функций называют неопределенным интегралом (от) функции  и обозначают символом
и обозначают символом 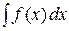 , т.е.
, т.е.
 ,
,
где 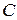 – произвольная постоянная, а
– произвольная постоянная, а  . (Коротко: неопределенный интеграл от функции
. (Коротко: неопределенный интеграл от функции  – это множество всех ее первообразных). При этом произведение
– это множество всех ее первообразных). При этом произведение 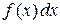 называют подынтегральным выражением, функцию
называют подынтегральным выражением, функцию  – подынтегральной функцией, а переменную
– подынтегральной функцией, а переменную 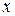 – переменной интегрирования.
– переменной интегрирования.
Заметим, что из равенства  следует, что выражение
следует, что выражение 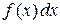 под знаком интеграла представляет собой дифференциал первообразной:
под знаком интеграла представляет собой дифференциал первообразной:
 .
.
Пример. Пусть  . Ее неопределенный интеграл равен
. Ее неопределенный интеграл равен
 .
.
Ответ проверяется просто: достаточно найти производную функции  .
.
Закономерен вопрос: какие функции интегрируемы? В дальнейшем будет установлено: если  (т.е. функция
(т.е. функция  непрерывна на
непрерывна на  ), то она имеет неопределенный интеграл. Пока же будет предполагаться, что существуют все рассматриваемые неопределенные интегралы.
), то она имеет неопределенный интеграл. Пока же будет предполагаться, что существуют все рассматриваемые неопределенные интегралы.
Дата публикования: 2015-09-17; Прочитано: 276 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
