 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Расстояние от точки до плоскости
|
|
Дана плоскость  и точка
и точка 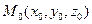 (см. рис).
(см. рис).

|
Опустим из точки 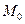 на плоскость перпендикуляр
на плоскость перпендикуляр 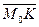 . Тогда
. Тогда  - это расстояние от точки до плоскости. Вектор нормали плоскости
- это расстояние от точки до плоскости. Вектор нормали плоскости  коллинеарен вектору
коллинеарен вектору 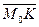 , следовательно,
, следовательно,  . Пусть точка
. Пусть точка  имеет координаты
имеет координаты  . Тогда
. Тогда
 .
.

Так как точка  принадлежит плоскости, то
принадлежит плоскости, то  и
и

Отсюда получаем формулу расстояния от точки до плоскости
 . (4.1)
. (4.1)
Пусть даны две плоскости:

Рассмотрим возможные случаи расположения плоскостей.
1. 

 - это условие параллельности плоскостей, если при этом еще и
- это условие параллельности плоскостей, если при этом еще и  , то плоскости совпадают.
, то плоскости совпадают.
Если плоскости параллельны, то можно найти расстояние между ними, для этого нужно воспользоваться формулой (4.1): 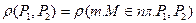 . Координаты точки
. Координаты точки  находим из уравнения плоскости
находим из уравнения плоскости  следующим образом: две координаты задаем произвольным образом, например,
следующим образом: две координаты задаем произвольным образом, например,
 , а третью координату находим из уравнения, следовательно,
, а третью координату находим из уравнения, следовательно,  .
.
2.  - это условие перпендикулярности плоскостей.
- это условие перпендикулярности плоскостей.
3. 
Пример. Составить уравнение плоскости, проходящей через точку  , параллельной плоскости
, параллельной плоскости  . Найти расстояние от точки
. Найти расстояние от точки  до плоскости
до плоскости  .
.
Решение. Так как искомая плоскость параллельна плоскости  , то в качестве ее вектора нормали можно взять вектор нормали плоскости
, то в качестве ее вектора нормали можно взять вектор нормали плоскости  , то есть
, то есть  . Воспользуемся уравнением:
. Воспользуемся уравнением:
 , или
, или
 .
.
Для нахождения расстояния от точки  до плоскости
до плоскости  воспользуемся формулой (4.1):
воспользуемся формулой (4.1):
 ,
,  .
.
Дата публикования: 2015-07-22; Прочитано: 248 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
