Пусть дано число a и вектор а

Df: Произведением числа a на вектор a называется вектор, такой, что:

1. |b|=|a|×|a|

2. b­­a, если a>0

b­¯a, если a<0

b=0, если a=0 или a=0

Из определения произведения вектора на число вытекают следующие 3 свойства

Свойства произведения вектора на число

1⁰. 1×a=a

2⁰. -1×a=-a

|(-1)×a|=|-1|×|a|=|a| и |-a|=|a| Þ |(-1)a|=|-a|

(-1) a­¯a и -a­¯a Þ (-1)a­­(-a)

3⁰. Любой вектор a можно представить в виде произведения модуля вектора а на его единичный вектор. a=|a|×a⁰

Докажем, что произведение вектора на число обладает следующим дополнительным свойством:

4⁰. Пусть a,b- два вектора и a¹0, тогда а коллинеарен b, тогда и только тогда, когда существует число a, такое, что b=a×a

a | | b Û$a такое, что b=a×a(a¹0)

Доказательство:

Пусть a | | b и a¹0 (1). Согласно 3⁰ вектор а можно представить:

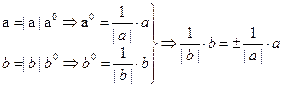
Из (1) следует b⁰= ± a⁰

Обозначим , значит

Из того, что b= a×a Þ a | | b

5⁰. Произведение вектора на число ассоциативно относительно произведения чисел

(ab)a=a(ba)

Доказательство:

Рассмотрим модуль вектора:

|(ab)a|=|ab|×|a|=|a|×(|b|×|a|)=|a| |ba|=|a(ba)|

Направление векторов, стоящих в левой и правой частях равенства также совпадают, т.к. они сонаправлены с a; а если a и b числа разных знаков, то они противоположно направлены с a.

6⁰. Дистрибутивный закон относительно суммы чисел (a+b)a=aa+ba –первый дистрибутивный закон

Доказательство:

Очевидно, равенство имеет в следующих случаях: если одно из чисел равно 0, или их сумма равна 0, или а=0. Эти случаи мы исключаем из рассмотрения.

Рассмотрим два случая.

А) a и b - одного знака

| (a+b) a|=|a+b|×|a|=(|a|+|b|)|a|=|a|×|a|+|b|×|a|=|aa|+|ba|=|aa + ba|

Направление векторов, стоящих в обеих частях равенства, также сонаправленны если a>0 Ù b>0, то оба вектора сонаправлены с а; если a<0 Ù b<0, то оба вектора противоположно направлены с а.

Б) a и b разных знаков

aа=(a+b-b)а=((a+b)+(-b))а=(a+b)а+(-b)а

Прибавим к обеим частям равенства bа:

aа+bа=(a+b)а+((-b)а+bа)=(a+b)а

7⁰.Произведение вектора на число дистрибутивно относительно суммы векторов a(a+b)=aa+ab – второй дистрибутивный закон

Равенство имеет место, если один из векторов нулевой, или их сумма равно 0, или a=0. Поэтому эти случаи исключим из рассмотрения.

Рассмотрим два случая:

А) a | | b

Построим ОА=a, OB=b, OA’=aa (a>0), OB’=a×OB=a(a+b)

Т.к. DOAB~DOA’B’ÞA’B’=aAB=ab

O,A’,B’ÞOB’=OA’+A’B’=aa+ab=a(a+b)

В) a | | bÞ$ b ÷ b=bb

a(a+b)=a(a+ba)=a((1+b)a)=(a(1+b))a=(a+ab)a=aa+(ab)a=aa+a(ba)=aa+ab

Лекция 3

Линейная зависимость векторов. Координаты вектора. Действия над векторами в координатах.

Упорядоченный набор бесконечного числа векторов (чисел) будем называть системой векторов (чисел).

Пусть дана система векторов: a_1, a₂,…, a_n (1)

и систем чисел:a_1,a₂,...a_n (2)

Тогда b=a₁a₁+a₂a₂+…+a_na_n называется линейной комбинацией векторов системы (1), определенной системой чисел (2). Будем так же говорить, что вектор b линейно выражается через вектора системы (1) (операции сложения, вычитания и умножения на число называются линейными операциями)

Df: Система векторов a_1, a₂,…, a_n называется линейной системой, если существует система чисел a_1,a₂,...a_n среди которых хотя бы одно отлично от нуля и такая, что выполняется равенство: a₁a₁+a₂a₂+…+a_na_n=0 (3)

Если равенство (3) возможно лишь при условии, когда:a₁₌a₂₌...₌a_n=0, то система называется линейно независимой

Теорема 1: если система векторов содержит нулевой вектор, то она линейно зависима

Доказательство:

Пусть а₁=0, тогда 1×a₁+0×a₂+…+0×a_n=0

Следствие: система, состоящая из одного вектора, линейно зависима, тогда и только тогда, когда вектор нулевой

Теорема 2: если система векторов содержит линейно зависимую подсистему, то она линейно зависима

Доказательство:

Пусть дана система векторов: a_1, a₂,…, a_n и пусть она имеет линейно зависимую подсистему: b_k=a_k, b_k+1=a_k+1,…,b_n=a_n. Тогда существуют числа: b_k,b_k+1,…,b_n, среди которых хотя бы одно отлично от нуля, например b_k 0, что будет выполняться равенство: b_kb_k+…+b_nb_n=0

a₁=a₂=…=a_k-1=0; a_k=b_k,…, a_n=b_n

Составим линейную комбинацию:

0×a₁+…+0×a_k-1+(a_ka_k+…+a_na_n)=0

Теорема 3: система векторов линейно зависима, тогда и только тогда, когда один вектор системы линейно выражается через остальные.

Доказательство:

1) Необходимость

Пусть система векторов (1) линейно зависима, тогда существует система чисел (2), среди которых хотя бы одно отлично от нуля. Пусть a₁ 0, и такая, что:

a₁a₁+a₂a₂+…+a_na_n=0

a₁=b₂a₂+…+b_na_n

2) Достаточность

Пусть вектор а линейно выражается через остальные вектора системы (1)

a₁=b₂a₂+…+b_na_n , тогда

(-1)a₁+b₂a₂+…+b_na_n=0

Следовательно система (1) линейно зависима

Следствие: если система векторов линейно независима, то ни один вектор этой системы нельзя выразить через остальные вектора системы

Теорема 4: система двух векторов линейно зависима тогда и только тогда, когда вектора коллинеарны

Доказательство:

1) Необходимость

Пусть пара векторов {a,b} линейно зависима Þ$a,b-числа ½a²+b²¹0, a×a+b×b

Пусть b¹0, тогда

2) Достаточность

Пусть a | | b. Если а=0, то система линейно зависима

Пусть а¹0, тогда

-линейно зависима

Df: Базисом плоскости называется упорядоченная пара линейно независимых векторов

Из Теоремы 4 следует, что базис плоскости образует упорядоченную пару неколлинеарных векторов B₁=(e₁,e₂), B₂=(e₂,e₁), B₁¹B₂

Базис называется ортогональным, если его вектора взаимно перпендикулярны

«B=(e₁,e₂) – ортогональный базис» Û e₁^e₂

«B=(e₁,e₂) – нормированный базис»Û |e₁|=|e₂|=1

«B=(e₁,e₂) – ортонормированный базис»Û

Для векторов ортогонального базиса вводятся обозначения: e₁=i, e₂=j

Теорема 5: любой вектор плоскости можно разложить по базису и притом единственным образом

Если на плоскости дан базис B=(e₁,e₂) и а – произвольный вектор плоскости, то существует единственная пара чисел (x,y) такая, что a=xe₁+ye₂

Доказательство:

Построим вектор OE₁=e₁, OE₂=e₂, OA=a (1), где О – произвольная точка плоскости

Построим:

A₁=OE₁ÇAA₁ | | OE₂ (2)

A₂=OE₂ÇAA₂ | | OE₁ (3)

(2), (3) Þ OA₁AA₂ – параллелограмм

OA=OA₁+OA₂ (4)

(2)ÞOA₁ | | e₁ Þ$x|OA₁=xe₁ (5)

(3)ÞOA₂ | | e₂ Þ$yOA₂=ye₂ (6)

Подставим (1), (5), (6) в (4):

a=xe₁+ye₂ (7)

Докажем, что пара (x,y) – единственная. Предположим, что существует другая пара (x^*,y^*) для которой a=x^*e₁+y^*e₂ (8)

Из (7) и (8)

Следствие: любые три вектора на плоскости линейно зависимы

Доказательство:

"a, b, c

1) если пара {a,b} – линейно зависима, то {a,b,c} – линейно зависима (Теорема 2)

2) {a,b} – линейно независима ÞB(a,b) – базис (Теорема 5) Þ $(x,y) | c=xa+ybÞ {a,b,c} –линейно зависимы (Теорема 3)

Df: Упорядоченная пара чисел, определяющая разложение вектора по базису называется координатами вектора в этом базисе