Плоскость в трехмерном пространстве

Теорема 6.1 Если в пространстве выбрана некоторая прямоугольная система координат, то уравнение первой степени относительно переменных .

(6.1)

Определяет в этой системе координат некоторую плоскость. (При условии, что коэффициенты не обращаются в нуль одновременно).

Найдется точка , координаты которой удовлетворяют уравнению (6.1).

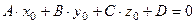. (6.2)

Вычитая уравнение (6.2) из (6.1), получим уравнение (6.3), эквивалентное исходному уравнению.

. (6.3)

Это уравнение есть условие ортогональности нормального вектора и вектора

,

начало которого в фиксированной точке , а конец в свободной точке с произвольными координатами и . Вектор может изменять длину и вращаться вокруг вектора , оставаясь перпендикулярным к нему. Свободная точка 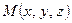, являющаяся концом вектора, будет при этом перемещаться по плоскости, проходящей через точку 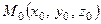перпендикулярно вектору .

Следовательно, уравнение (6.3) есть уравнение плоскости с нормальным вектором , проходящей через фиксированную точку . Теорема доказана.

Уравнение (6.1), эквивалентное уравнению (6.3), называется общим уравнением плоскости.

Рассмотрим неполные уравнения плоскости при условии :

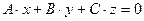1) . Уравнение определяет плоскость, проходящую через начало координат.

2) . Уравнение определяет плоскость, параллельную оси , так как её нормальный вектор перпендикулярен оси .

3) . Уравнение определяет плоскость, перпендикулярную оси , так как её нормальный вектор параллелен оси .

Остальные неполные уравнения плоскости рассматриваются аналогично.

Уравнение плоскости «в отрезках» легко получить из уравнения (6.1), если перенести свободный член направо от знака равенства, разделить на него левую часть уравнения и сделать очевидные алгебраические преобразования:

. (6.4)

Введем обозначения , уравнение (6.4) примет следующий вид:

. (6.5)

Уравнение (6.5) имеет смысл при условиях и .

Здесь числа и равны координатам точек пересечения плоскости с осями координат.

Убедиться в этом можно, решив систему уравнений, состоящую из уравнения плоскости (6.5) и уравнений осей координат, например оси :

. (6.6)

Доказательства для точек и проводятся аналогично.

Угол между плоскостями и условия параллельности и перпендикулярности плоскостей очевидным образом связаны с соответствующими условиями для их нормальных векторов

Пусть заданы уравнения двух плоскостей

(6.7)

Угол между плоскостями равен углу между нормальными векторами этих плоскостей. В данном случае это вектора

и

Косинус угла между векторами можно найти исходя из определения скалярного произведения

. (6.8)

Условие ортогональности плоскостей следует из условия ортогональности их нормальных векторов, то есть равенства нулю их скалярного произведения:

. (6.9)

Условия параллельности плоскостей следуют из условия коллинеарности их нормальных векторов:

. (6.10)

Задача 6.1. Составить уравнение плоскости, проходящей через три заданные точки.

Пусть заданы точки

,

не принадлежащие одной прямой. Тогда вектора

и

не будут коллинеарными. Пусть точка 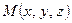«свободная точка» с произвольными координатами , а вектор

«свободный вектор». Чтобы точка 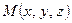принадлежала плоскости, определяемой векторами и необходимо и достаточно, чтобы все три вектора были компланарны, а их смешанное произведение равнялось нулю.

(6.11)