Следствие 2

(4.11)

Определение 4.2. Векторным произведением вектора на вектор называется вектор 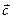, обозначаемый символом

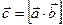и удовлетворяющий трем требованиям:

(Квадратным скобками обозначают векторное произведение.)

1) вектор 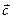ортогонален к каждому из векторов и ,

2) длина вектора 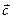равна произведению модулей перемножаемых векторов на синус угла между ними.

(4.12)

3) упорядоченная тройка векторов является правой.

Определение 4.3. У порядоченная тройка некомпланарных векторов является правой, если, после приведения векторов к общему началу, вектор 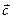располагается так, что из его конца кратчайший поворот от к виден происходящим в направлении против часовой стрелки. (В противном случае тройка векторов считается левой.)

Это утверждение справедливо для тройки векторов и для системы декартовых координат в пространстве.

Векторное произведение имеет следующие алгебраичес-кие свойства:

1) , (антиперестановочность)

2) ,

3) ,

4) .

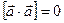Теорема 4.3. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Доказательство. Если и , то доказательство необходимости и достаточности утверждения теоремы следует из (4.12) и того факта, что условие при 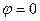также является необходимым и достаточным.

Теорема 4.4. Модуль векторного произведения равняется площади параллелограмма, построенного на приведенных к общему началу векторах и .

Доказательство. Поскольку площадь параллелограмма равна произведению длин его смежных сторон на синус угла между ними, доказательство теоремы следует из формулы (4.12).

Теорема 4.5. Если вектора представлены разложениями но базису

, (4.13)

то их векторное произведение имеет вид:

(4.14)

Доказательство. Перемножив векторные многочлены (4.13), получим, что

Строка (4.15) последнего выражения получена с учетом того, что

(4.16)

(Знак минус в этих произведениях получается вследствие нарушения порядка в тройке ортов .)

Очевидно, что выражение (4.15) есть разложение определителя (4.14) по элементам первой строки.

Теорема доказана.

Следствие. Если два вектора и коллинеарны, то координаты их пропорциональны, т.е.

(4.17)

Доказательство. Поскольку векторное произведение коллинеарных векторов равно нулю, из соотношения (4.15) следует, что

(4.18) Из первого равенства после деления на произведение получим пропорцию . Аналогичным образом из второго равенства получаем пропорцию .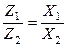

Следствие доказано.

В пропорции (4.17) возможно появление нулей в знаменателе. В соответствии с (4.18) это означает, что соответствующий числитель тоже равен нулю.

Для последующих выкладок нам удобно считать, что .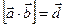

Следствие 1. Если −орт вектор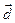а , а −площадь параллелограмма, построенного на перемножае-мых векторах, приведенных к общему началу, то

(4.19)

Определение 4.4. Если векторное произведение умножитьскалярно на вектор , то число называется смешанным произведением векторов и .

Теорема 4.6. Смешанное произведение равно объёму параллелепипеда, построенного на приведенных к общему началу векторах и , взятому со знаком плюс, если тройка векторов правая, и со знаком минус, если тройка левая. Если же перемножаемые вектора компланарны, то их смешанное произведение ровно нулю.

Доказательство. Тривиальный случай коллинеарности векторов и исключим, так как векторное произведение коллинеарных векторов равно нулю. Тогда, используя выражение (4.19), можно произвести следующее преобразование (4.20)

(Знак + берем в случае, если тройка векторов правая).

Если же вектора и компланарны, то вектор лежит в плоскости векторов и , следовательно и .

Теорема доказана.

Следствие 1. Справедливо равенство

(4.21)

Объём параллелепипеда не зависит от того, какая пара векторов из тройки перемножается векторно. Знак произведения не изменяется, так как сохраняется порядок векторов и ориентация тройки векторов.

Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.

Теорема 4.7. Если три вектора представлены разложениями по базису

,

то их смешанное произведение равно следующему определителю:

(4.22)

Доказательство. Из формулы (4.15) следует, что:

Умножив скалярно этот вектор на вектор , получим,

(4.23)

Полученное выражение (4.23) есть разложение определителя (4.22) по элементам третьей строки. Теорема доказана.

Задачи № 795, 800, 803, 812, 818, 820, 829, 834, 840, 847, 851, 858, 875, 877.

Вопросы для повторения

1. Скалярное произведение, определение. Геометрические и алгебраические свойства.

2. Скалярное произведение в декартовых координатах, (доказать).

3. Угол между векторами, условия перпендикулярности векторов.

4. Проекция одного вектора на другой или на произвольную ось.

5. Определение векторного произведения. Тройка векторов. Геометрические и алгебраические свойства векторного произведения.

6. Векторное произведение в декартовых координатах (доказать).

7. Условия коллинеарности векторов (доказать)

8. Смешанное произведение 3-х векторов. Геометрическая интерпретация (доказать). Условие компланарности 3-х векторов.

9. Смешанное произведение 3-х векторов в декартовых координатах (доказать).