Произведения векторов

Определение 4.1. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

(4.1)

(Скалярное произведение принято обозначать круглыми скобками.)

Используя представление проекции вектора на другой вектор, можно записать

(4.2)

Теорема 4.1. Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.

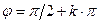Доказательство. Если оба вектора ненулевые, то доказательство необходимости и достаточности утверждения теоремы следует из того факта, что необходимым и достаточным условием равенства нулю является условие , то есть

(4.3)

Скалярное произведение имеет следующие свойства:

1) ,

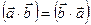2) , где 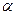− число,

3)

4) , если , , если .

Эти свойства позволяют при скалярном перемножении векторных многочленов выполнять действия почленно, вынося за скобки числовые множители.

Теорема 4.2. Проекция вектора на вектор равна скалярному произведению вектора на орт вектор .

Доказательство. Из соотношения (4.2) следует, что

(4.4)

Теорема 4.2. Если вектора и представлены в виде разложений по базису ,

, (4.5)

то скалярное произведение этих векторов равно следующему выражению:

(4.6)

Доказательство. Перемножив векторные многочлены (4.5), получим:

(4.7)

поскольку

(4.8)

а остальные скалярные произведения ортов , ввиду их ортогональности, обращаются в нули.

Следствие 1.

(4.9)

Здесь орт вектора

(4.10)