Система двух линейных уравнений с двумя неизвестными. Теорема Крамера

Система уравнений имеет вид,

(1.5)

Здесь и неизвестные, а коэффициенты и свободные члены и заданные числа.

Решением системы является пара чисел 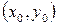, подстановка которых в уравнения системы (1.5) обращает эти уравнения в тождества.

Умножив первое уравнение на , а второе на и сложив полученные выражения, получим

(1.6)

Аналогично, умножая уравнения системы на и и

складывая полученные выражения, будем иметь,

(1.7)

Введем следующие обозначения:

(1.8)

В новых обозначениях выражения (1.6) и (1.7) будут иметь вид:

и (1.9)

Определитель принято называть определителем системы. Из соотношений (1.9) просто получаются формулы Крамера

и (1.10)

Могут представиться два случая: 1) определитель системы отличен от нуля. 2) определитель равен нулю.

В случае решение системы существует и единственно, так как система уравнений (1.9) является следствием системы (1.5).

Формулы (1.10) позволяют легко найти значения и .

Рассмотрим случай . Здесь имеют место два подслучая: а) хотя бы один из определителей или отличен от нуля,

б) оба определителя и равны нулю.

В подслучае а) хотя бы одно из равенств (1.10) не имеет смысла, и система (1.9), а вместе с ней и система (1.5) не имеет решений.

В подслучае б) система (1.5) имеет бесконечно много решений.

В самом деле, из равенства заключаем, (См. (1.4)) что (1.11)

Это означает, что второе уравнение системы (1.5) является следствием первого и может быть отброшено. Но линейное уравнение вида имеет бесконечно много решений, так как задав значение , из уравнения можно найти соответствующее значение , и таких пар чисел существует бесконечно много.

Приведенные выше утверждения составляют содержание теоремы Крамера, которую можно сформулировать так:

Если определитель системы (1.5) отличен от нуля, то существует и притом единственное, решение этой системы, определяемое формулами Крамера (1.10 )

Если определитель системы (1.5) , то система либо вовсе не имеет решений (если хотя бы один из определителей или отличен от нуля), либо имеет бесконечно много решений (в случае ).

Замечание: В случае, когда и система называется однородной. Однородная система всегда имеет тривиальное решение . Если определитель системы отличен от нуля, система имеет только тривиальное решение.

Если же то однородная система имеет бесконечно много решений

. Таким образом, однородная система уравнений имеет нетривиальные решения в том и только в том случае, если её определитель равен нулю.

Уравнения системы (1.5) являются уравнениями прямых на плоскости. Числа и , определяемые по формулам Крамера (1.10) при являются координатами точки пересечения этих прямых. В случае однородной системы уравнений точка пересечения прямых совпадает с началом координат ().

В случае прямые, описываемые системой (1.5) сливаются в одну, и все точки этой прямой образуют бесконечное множество решений системы. Это утверждение справедливо для однородной и неоднородной систем.

Если же при , или , то прямые, описываемые системой (1.5) параллельны (система не имеет решений). В случае однородной системы это невозможно, так как обе прямые проходят через начало координат.