 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Контрольная работа 1. Часть 1
|
|
При выполнении контрольных заданий обязательно указывать название темы и номер задания, даже если задание не выполнено.
Вариант 1.1
Задание 1. Определить скалярное произведение  векторов, если
векторов, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 2. Вычислить 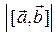 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
,  ,
,  .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки 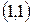 и
и  .
.
Задание 5. Написать уравнение плоскости, проходящей через две точки  ,
,  перпендикулярно плоскости
перпендикулярно плоскости  .
.
Задание 6. Написать уравнение плоскости, проходящей через три точки с координатами  ,
,  ,
,  .
.
Задание 7. Вывести каноническое уравнение параболы, если известно, что ее вершина расположена в начале координат, она расположена симметрично оси  , и проходит через точку
, и проходит через точку  .
.
Вариант 1.2
Задание 1. Определить скалярное произведение  векторов, если
векторов, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 2. Вычислить 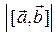 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
,  ,
, 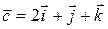 .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки  и
и  .
.
Задание 5. Составить уравнение прямой, проходящей через точку 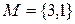 параллельно прямой
параллельно прямой  .
.
Задание 6. Найти точку пересечения плоскости  с прямой, заданной каноническими уравнениями:
с прямой, заданной каноническими уравнениями:  .
.
Задание 7. Написать уравнение гиперболы, если ее фокусы находятся в точках  ,
, 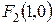 , а длина ее действительной оси равна 8.
, а длина ее действительной оси равна 8.
Вариант 1.3
Задание 1. Определить скалярное произведение  векторов, если
векторов, если  ,
, 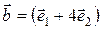 ,
,  ,
,  ,
,  .
.
Задание 2. Вычислить 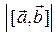 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
,  ,
,  .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки  и
и  .
.
Задание 5. Составить уравнение прямой, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой  .
.
Задание 6. Найти точку пересечения плоскости  с прямой, заданной каноническими уравнениями:
с прямой, заданной каноническими уравнениями:  .
.
Задание 7. Найти координаты фокусов и эксцентриситет эллипса, описываемого уравнением  .
.
Вариант 1.4
Задание 1. Определить скалярное произведение  векторов, если
векторов, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 2. Вычислить 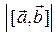 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
,  ,
,  .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки  и
и  .
.
Задание 5. Вычислить площадь квадрата, если две его стороны лежат на прямых  и
и  .
.
Задание 6. Найти точку пересечения плоскости  с прямой, заданной общими уравнениями:
с прямой, заданной общими уравнениями:
 .
.
Задание 7. Найти центр и радиус окружности, заданной уравнением  .
.
Вариант 1.5
Задание 1. Определить скалярное произведение  векторов, если
векторов, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 2. Вычислить 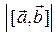 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
, 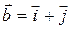 ,
,  .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки  и
и  .
.
Задание 5. По известным координатам вершин треугольника  ,
,  ,
, 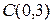 записать для его сторон уравнения в общем виде и уравнение в общем виде биссектрисы угла
записать для его сторон уравнения в общем виде и уравнение в общем виде биссектрисы угла  .
.
Задание 6. Найти точку пересечения плоскости  с прямой, заданной каноническими уравнениями:
с прямой, заданной каноническими уравнениями:  .
.
Задание 7. Найти координаты фокусов, вершин и уравнения асимптот гиперболы  .
.
Вариант 1.6
Задание 1. Определить скалярное произведение  векторов, если
векторов, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 2. Вычислить 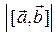 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
,  ,
,  .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки  и
и  .
.
Задание 5. Написать уравнение плоскости, проходящей через точку  параллельно плоскости
параллельно плоскости  .
.
Задание 6. Найти точку пересечения плоскости  с прямой, заданной общими уравнениями:
с прямой, заданной общими уравнениями:
 .
.
Задание 7. Написать уравнение гиперболы, если ее фокусы находятся в точках  и
и  , а длина действительной полуоси равна
, а длина действительной полуоси равна  .
.
Вариант 1.7
Задание 1. Определить скалярное произведение  векторов, если
векторов, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 2. Вычислить 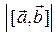 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
,  ,
,  .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки  и
и  .
.
Задание 5. Написать уравнение плоскости, проходящей через точку  параллельно плоскости
параллельно плоскости  .
.
Задание 6. Вычислить расстояние от точки 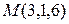 до прямой
до прямой  .
.
Задание 7. Найти координаты фокусов, вершин и уравнение асимптот гиперболы  .
.
Вариант 1.8
Задание 1. Определить скалярное произведение  векторов, если
векторов, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 2. Вычислить 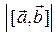 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
,  ,
,  .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки 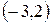 и
и  .
.
Задание 5. Написать уравнение плоскости, проходящей через точку  параллельно векторам
параллельно векторам  и
и  .
.
Задание 6. Найти уравнение прямой, проходящей через точки  и
и  .
.
Задание 7. Найти полуоси, координаты фокусов, уравнения директрис и эксцентриситет эллипса  .
.
Вариант 1.9
Задание 1. Определить скалярное произведение  векторов, если
векторов, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 2. Вычислить 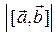 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
,  ,
,  .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки  и
и  .
.
Задание 5. Написать уравнение плоскости, проходящей через три точки с координатами  ,
,  ,
,  .
.
Задание 6. Написать канонические и параметрические уравнения прямой, образованной пересечением плоскостей  и
и  .
.
Задание 7. Написать каноническое уравнение параболы, расположенной симметрично оси 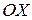 , имеющей вершину в начале координат и проходящей через точку
, имеющей вершину в начале координат и проходящей через точку  .
.
Вариант 1.10
Задание 1. Определить скалярное произведение  векторов, если
векторов, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 2. Вычислить 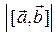 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
,  ,
,  .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки  и
и  .
.
Задание 5. Написать уравнение плоскости, проходящей через две точки  ,
,  перпендикулярно плоскости
перпендикулярно плоскости  .
.
Задание 6. Вывести общее уравнение плоскости, проходящей через точку  параллельно векторам
параллельно векторам  и
и  .
.
Задание 7. Найти полуоси, координаты фокусов, уравнения директрис и эксцентриситет эллипса  .
.
3.1. Пример выполнения контрольной работы 1 (часть 1)
Задание 1. Определить скалярное произведение  векторов, если
векторов, если 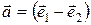 ,
,  ,
,  ,
,  ,
,  .
.
Решение: Подставим в скалярное произведение выражения векторов через их базисы:  , по свойствам скалярного произведения, имеем:
, по свойствам скалярного произведения, имеем:


 . Ответ:
. Ответ:  .
.
Задание 2. Вычислить 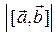 , если
, если  ,
,  ,
,  ,
,  ,
,  .
.
Решение: Исходные вектора заданы через аффинный базис, поэтому, запишем их векторное произведение через соответствующие базисные вектора:  {используя свойства векторного произведения, имеем}
{используя свойства векторного произведения, имеем}  . Ответ:
. Ответ: 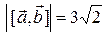 .
.
Задание 3. Определить смешанное произведение  , если
, если  ,
,  ,
,  .
.
Решение: Так как векторы заданы в декартовом базисе, то смешанное произведение находится по формуле:

 .
.
Ответ:  .
.
Задание 4. Вывести общее уравнение прямой, проходящей через точки 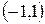 и
и  .
.
Решение: Обозначим точку с координатами 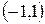 как
как  , а точку с координатами
, а точку с координатами  как
как  , тогда каноническое уравнение прямой, проходящей через данные точки запишется в виде:
, тогда каноническое уравнение прямой, проходящей через данные точки запишется в виде:  .
.
Преобразуем полученное уравнение: 
 .
.
Ответ:  .
.
Задание 5. Написать общее уравнение плоскости, проходящей через точку  параллельно оси
параллельно оси 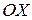 и перпендикулярно к плоскости
и перпендикулярно к плоскости  .
.
Решение: Обозначим нормаль плоскости  как
как 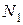 , а нормаль искомой плоскости как
, а нормаль искомой плоскости как 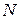 . Так как искомая плоскость по условию задачи перпендикулярна плоскости
. Так как искомая плоскость по условию задачи перпендикулярна плоскости  , то их нормали будут также перпендикулярны
, то их нормали будут также перпендикулярны  .
.
Возьмем на оси 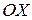 единичный вектор
единичный вектор  . По условию искомая плоскость параллельна оси
. По условию искомая плоскость параллельна оси 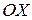 , значит, ее нормаль и единичный вектор будут перпендикулярны
, значит, ее нормаль и единичный вектор будут перпендикулярны  .
.
По определению векторного произведения имеем:

 , откуда
, откуда  .
.
Подставим в общее уравнение плоскости координаты ее точки и нормали, получаем:  или
или  .
.
Ответ:  .
.
Задание 6. Вывести общее уравнение плоскости, проходящей через точку  параллельно векторам
параллельно векторам  и
и  .
.
Решение: Пусть нормаль искомой плоскости есть  . По условию задачи искомая плоскость параллельна заданным векторам, следовательно, ее нормаль перпендикулярна к ним:
. По условию задачи искомая плоскость параллельна заданным векторам, следовательно, ее нормаль перпендикулярна к ним:  и
и  , и откуда следует, что нормаль есть их векторное произведение:
, и откуда следует, что нормаль есть их векторное произведение:
 ,
,  , откуда координаты нормали:
, откуда координаты нормали:  . Подставим найденные координаты нормали и координаты фиксированной точки
. Подставим найденные координаты нормали и координаты фиксированной точки  в общее уравнение плоскости, получим:
в общее уравнение плоскости, получим:  , или
, или  .
.
Ответ:  .
.
Задание 7. Для гиперболы  найти действительную и мнимую полуоси, координаты фокусов и эксцентриситет.
найти действительную и мнимую полуоси, координаты фокусов и эксцентриситет.
Решение: Приведем исходное уравнение к каноническому виду:  или
или  , откуда действительная полуось
, откуда действительная полуось  , мнимая полуось
, мнимая полуось  , эксцентриситет
, эксцентриситет  , координаты фокусов определяются значением величины
, координаты фокусов определяются значением величины  :
:  и
и  . Ответ:
. Ответ: 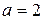 ,
,  ,
,  ,
,  ,
,  .
.
Дата публикования: 2015-07-22; Прочитано: 671 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
