Примеры решения типовых задач: прямая в пространстве

Задача 2.12

Написать канонические и параметрические уравнения прямой, образованной пересечением плоскостей и .

Решение: 1)Найдем координаты фиксированной точки. Из исходной системы уравнений исключим . Положим , тогда: , откуда находим: , . Таким образом, нашли координаты фиксированной точки .

2) Направляющий вектор определяется как векторное произведение нормалей двух плоскостей, образующих прямую:

.

3) Запишем канонические уравнения: , или .

4) Обозначив , получаем параметрические уравнения:

, , .

Задача 2.13

Найти уравнение прямой, проходящей через точки и .

Решение: 1)Возьмем в качестве фиксированной точки точку , тогда направляющий вектор определится как .

2)Тогда канонические уравнения прямой запишутся как . 3) В случае, когда в знаменателе канонических уравнений получается нуль, полагают равным нулю числитель, то есть одна из плоскостей определится уравнением: . Ответ: .

Задача 2.14

Вычислить расстояние от точки до прямой .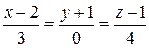

Решение: 1)Для определения расстояния необходимо знать координаты фиксированной точки прямой и ее направляющий вектор, что можно определить сразу из заданного уравнения прямой: и 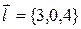, тогда радиус-вектор фиксированной точки прямой , а длина . 2) Радиус-вектор исходной точки , тогда 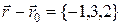. 3) Найдем векторное произведение:

,

откуда .

4) Подставляем в формулу определения расстояния (2.4) найденные значения: . Ответ: .

Задача 2.15

Найти точку пересечения плоскости с прямой, заданной общими уравнениями:

.

Решение: Решение сводится к решению системы трех уравнений с тремя неизвестными: , откуда находим , , .

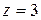Ответ: .

Задача 2.16

Найти точку пересечения плоскости с прямой, заданной каноническими уравнениями: .

Решение: Можно было бы перейти от канонических уравнений к общему виду и свести задачу к рассмотренной в предыдущем примере. Но можно рассуждать и по-другому. Точка пересечения должна принадлежать и прямой и плоскости, то есть можно подставить выражения для из канонического уравнения в уравнение плоскости и определить их.

1. Перейдем к параметрическим уравнениям прямой:

, откуда , , .

2. Подставим найденные выражения в уравнение плоскости:

, откуда .

3. Подставляем в выражения для , находим ответ: , , . Ответ: искомая точка .