 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Примеры решения типовых задач: уравнение плоскости
|
|
Задача 2.6
Написать уравнение плоскости, проходящей через точку  параллельно плоскости
параллельно плоскости  .
.
Решение: 1)По условию, плоскость должна быть параллельна плоскости  , а это значит, ее уравнение принимает вид:
, а это значит, ее уравнение принимает вид:  , где
, где 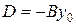 . 2) Нормаль этой плоскости должна быть
. 2) Нормаль этой плоскости должна быть  , где
, где  , откуда
, откуда  , следовательно, общее уравнение принимает вид:
, следовательно, общее уравнение принимает вид:  , или
, или  (по условию
(по условию  ). Ответ:
). Ответ:  .
.
Задача 2.7
Написать уравнение плоскости, проходящей через точку  параллельно плоскости
параллельно плоскости  .
.
Решение: 1)У параллельных плоскостей – общая нормаль, следовательно, для искомой плоскости нормаль 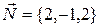 . 2) По формуле (2.1) получаем:
. 2) По формуле (2.1) получаем:  , или
, или  .
.
Ответ:  .
.
Задача 2.8
Написать уравнение плоскости, проходящей через точку  параллельно векторам
параллельно векторам  и
и  .
.
Решение: 1) Для решения необходимо знать координаты точки, принадлежащей искомой плоскости и нормаль к ней. Точка  – известна, осталось найти нормаль. 2) Так как по условию, искомая плоскость должна быть параллельна векторам, то ее нормаль должна быть к ним перпендикулярна:
– известна, осталось найти нормаль. 2) Так как по условию, искомая плоскость должна быть параллельна векторам, то ее нормаль должна быть к ним перпендикулярна:  и
и 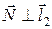 . 3) По свойству векторного произведения: если
. 3) По свойству векторного произведения: если  , то
, то  и
и  , значит в нашем случае, нормаль к исходным векторам есть их векторное произведение:
, значит в нашем случае, нормаль к исходным векторам есть их векторное произведение:  , откуда координаты нормали:
, откуда координаты нормали:  . 4) Подставляем найденные координаты и координаты фиксированной точки в уравнение (2.1), находим общее уравнение:
. 4) Подставляем найденные координаты и координаты фиксированной точки в уравнение (2.1), находим общее уравнение:  . После преобразования получим Ответ:
. После преобразования получим Ответ:  .
.
Задача 2.9
Написать уравнение плоскости, проходящей через три точки с координатами 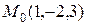 ,
,  ,
,  .
.
Решение: 1)Проведем к точкам соответствующие радиус-векторы:  ,
,  и
и  . 2) Очевидно, что вектора
. 2) Очевидно, что вектора  и
и 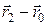 будут лежать в одной плоскости и задача сводится к задаче, приведенной в предыдущем примере. 3) Координаты векторов:
будут лежать в одной плоскости и задача сводится к задаче, приведенной в предыдущем примере. 3) Координаты векторов:


4) Найдем координаты нормали:

5) Подставляем найденные координаты и координаты фиксированной точки  в уравнение (2.1), находим общее уравнение:
в уравнение (2.1), находим общее уравнение:
 . Ответ:
. Ответ:  .
.
Задача 2.10
Написать уравнение плоскости, проходящей через две точки  ,
,  перпендикулярно плоскости
перпендикулярно плоскости 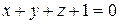 .
.
Решение: 1)Для определенности положим, что  – фиксированная точка, радиус-вектор которой
– фиксированная точка, радиус-вектор которой  ;
;  – точка, с помощью которой строим вектор
– точка, с помощью которой строим вектор  , лежащий в искомой плоскости. Его координаты:
, лежащий в искомой плоскости. Его координаты:  . 2) Нормаль
. 2) Нормаль  плоскости
плоскости 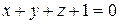 имеет координаты
имеет координаты  , что следует из вида общего уравнения плоскости (2.2). 3) Нормаль искомой плоскости перпендикулярна вектору
, что следует из вида общего уравнения плоскости (2.2). 3) Нормаль искомой плоскости перпендикулярна вектору  и нормали плоскости
и нормали плоскости  , то есть является их векторным произведением:
, то есть является их векторным произведением:  . Откуда:
. Откуда:
 , или
, или  .
.
4) Подставим в общее уравнение плоскости (2.2) найденные значения координат нормали и фиксированной точки:  .
.
Ответ:  .
.
Задача 2.11
Записать уравнение плоскости, проходящей через точки  ,
,  и образующей с плоскостью
и образующей с плоскостью  угол равный
угол равный  .
.
Решение: 1)Для определенности положим, что  – фиксированная точка, радиус-вектор которой
– фиксированная точка, радиус-вектор которой 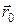 ;
;  – точка, с помощью которой строим вектор
– точка, с помощью которой строим вектор  , лежащий в искомой плоскости. Его координаты:
, лежащий в искомой плоскости. Его координаты: 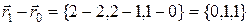 .
.
2) Так как нормаль  искомой плоскости перпендикулярна этому вектору
искомой плоскости перпендикулярна этому вектору  , то
, то  . Скалярное произведение в декартовой системе координат определяется по формуле:
. Скалярное произведение в декартовой системе координат определяется по формуле:  , откуда получаем уравнение
, откуда получаем уравнение 
3) Нормаль  плоскости
плоскости  имеет координаты
имеет координаты  . Подставим известные значения в формулу (2.4):
. Подставим известные значения в формулу (2.4):
 ,
,
или  .
.
1. Итак, имеем систему из двух уравнений относительно трех неизвестных:  .
.
2. Уменьшим число неизвестных, для чего разделим обе части на  :
:
 ,
,
3. Подставим выражение из первого уравнения во второе, получим:
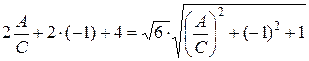 , откуда
, откуда  .
.
4. Получили пропорцию коэффициентов нормали:  , откуда в качестве координат нормали возьмем
, откуда в качестве координат нормали возьмем  .
.
5. Уравнение плоскости запишется в виде:
 . Ответ:
. Ответ:  .
.
Дата публикования: 2015-07-22; Прочитано: 773 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
