Уравнение прямой на плоскости

Рассмотрим точку с координатами и ненулевой вектор (2.3).

Рис. 2.3. Радиус – векторы точек

Обозначим точкой – начало координат, точка с координатами – переменная точка, лежащая на прямой, проведенной через точку перпендикулярно вектору 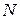. Тогда соединяя точки и с началом координат , получим радиус – векторы точек – и , и .

Вектор перпендикулярен вектору 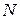, следовательно, их скалярное произведение равно 0:

.

(2.1)

Данное уравнение называется уравнением прямой через ее нормаль. Перепишем данное уравнение в координатной форме: . Точка – неподвижна, обозначив выражение 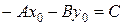, получим общее уравнение прямой:

.

(2.2)

Еще раз напомним геометрический смысл величин, входящих в уравнение: – координаты вектора , перпендикулярного к исходному вектору, проходящему через точку с координатами . Свободный член .

Так как в общее уравнение входят только первые степени и , то говорят, что прямая на плоскости есть линия первого порядка.

Данное уравнение связывает координаты линии и перпендикуляра к ней. Но точно также можно построить уравнение, связывающее две параллельные прямые.

Проведем параллельно прямой, проходящей через точку вектор , который называется направляющим вектором прямой. Так как коллинеарные вектора отличаются друг от друга только величиной некоторого скаляра (обозначим его ), то тогда можно записать следующее уравнение, которое называется параметрическим уравнением прямой:

.

(2.3)

Или переписав в координатной форме, имеем: , исключив параметр , получаем каноническое уравнение прямой:

.

(2.4)

В частности, если прямая проходит через две заданные точки с координатами и , то каноническое уравнение можно переписать в виде:

.

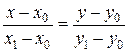(2.5)

Разрешим общее уравнение прямой относительно переменной и, приняв условие, что , получим следующее уравнение:

,

(2.6)

где , при . Данное уравнение называется уравнением прямой с угловым коэффициентом и позволяет определить всякую прямую, расположенную под углом, относительно исходной. Коэффициент – есть тангенс угла наклона прямой к оси (Рис. 2.4), – ордината точки пересечения прямой с осью .

Рис. 2.4. Коэффициент 2 – есть тангенс угла наклона прямой к оси

Как правило, уравнение с угловым коэффициентом используют в несколько другой форме. Пусть на прямой имеется некоторая точка с известными координатами , тогда уравнение этой прямой можно записать: , откуда , тогда уравнение прямой запишется в виде: , или

.

(2.7)

Вернемся к общей форме уравнения прямой (2.2). При условии, что , разделим все члены уравнения на свободный член: , обозначив и , получаем уравнение прямой в отрезках:

.

(2.8)

При имеем , а при соответственно . Таким образом, числа и есть отрезки, отсекаемые прямой на осях координат.

Если две прямые заданы своими уравнениями в общем виде: и , то угол между ними можно определить по формуле:

,

(2.9)

а если прямые заданы в виде и , то по формуле:

.

(2.10)

Расстояние от точки до прямой находится по формуле:

.

(2.11)

При решении задач, прежде всего, обращают внимание на известные величины и в зависимости от них составляют уравнение прямой. Или, наоборот, по известному уравнению анализируют геометрические свойства прямой.