 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пример 1.2
|
|
Даны два вектора  и
и  . Доказать, что они могут быть базисом.
. Доказать, что они могут быть базисом.
Решение:
1. По определению вектора могут быть базисом, если они ненулевые и неколлениарны, поэтому для доказательства нужно проверить выполнение 3 свойства – соотношение координат векторов не должно быть равным.
2.  равенство неверно, значит, вектора
равенство неверно, значит, вектора 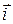 и
и  неколлениарны.
неколлениарны.
Ответ: вектора 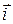 и
и  являются базисом.
являются базисом.
Дата публикования: 2015-07-22; Прочитано: 449 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
