Примеры решения типовых задач: векторная алгебра

Задача 1.1.

Даны два вектора и . Найти координаты вектора .

Решение: Из свойства 1 следует, что , следовательно: .

Ответ: .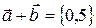

Задача 1.2

Найти координаты вектора , соединяющего точку с координатами и точку с координатами .

Решение: Обозначим координаты точки как , координаты точки как . Из свойства 2 следует: вектор имеет координаты . Подставляем исходные значения: .

Ответ: .

Задача 1.3

Доказать, что два вектора и коллинеарны.

Решение: Из свойства 3 следует, что для решения необходимо проверить выполнение равенства: . Подставим заданные значения координат: 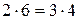, откуда: . Равенство верно.

Ответ: исходные вектора коллинеарны.

Задача 1.4

Задан вектор и известно, что точка имеет координаты . Найти координаты точки 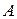– начала вектора.

Решение: Введем обозначения: – координаты вектора , – координаты точки , – координаты точки .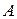

1. Из свойства 2 следует, что для решения необходимо решить два уравнения: ; .

2. Подставим известные величины: ; ; откуда искомые координаты: ; . Ответ: точка 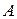имеет координаты .

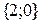Задача 1.5

Найти , если и , где , , угол .

Решение: Для решения необходимо знать длину векторов, что нам неизвестно, но даны данные по базису, поэтому перейдем от исходных векторов к базисным, подставим в формулу 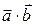выражения разложения векторов по базису:

1. Преобразуем скалярное произведение согласно 2 и 6 свойству:

2. Приведем подобные члены в полученном выражении и применим 3-е свойство скалярного произведения:

3. Вставим исходные данные и распишем формулу скалярного произведения базисных векторов:

. Ответ: 99.

Задача 1.6

Для векторов и найти их проекции друг на друга: и в декартовой системе координат.

Решение: Для определения проекции найдем скалярное произведение векторов; для декартовой системы координат справедлива формула: . Подставляем исходные координаты: . Найдем длину , из формулы для декартовых координат имеем: . Подставим найденные значения в искомую формулу: . Аналогично найдем вторую проекцию: 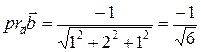. Ответ: ; .

Задача 1.7

Определить в декартовой системе координат угол между вектором с координатами {4, 1, 1} и вектором с координатами {2, 2, -1}.

Решение: Для вычисления угла по формуле необходимо определить длины векторов и их скалярное произведение.

. Определяем длины векторов ; 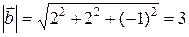. Подставляем в формулу: . Решая данное тригонометрическое уравнение, получим: . Ответ: .

Перед рассмотрением таких операций над векторами, как векторное и смешанное произведения, введем понятие определителя. С помощью определителя векторное и смешанное произведения можно представить через координаты векторов.

Задача 1.8

Определить длину вектора , если координаты вектора и вектора заданы в декартовой системе координат.

Решение: Сначала находим координаты вектора по формуле для определителя:

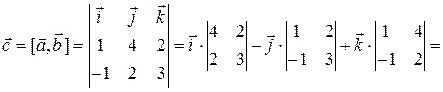
. Теперь по формуле вычисления длины вектора через его декартовы координаты имеем: .

Ответ: .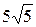

Задача 1.9

Найти длину вектора , если координаты вектора и вектора заданы в аффинной системе координат с базисом: , , .

Решение: Разложим исходные вектора по базису: ; . Подставим в выражение для и используем свойства векторного произведения:

.

По формуле длины векторного произведения имеем:

. Ответ: .

Задача 1.10

Вычислить площадь параллелограмма, две стороны которого образованы векторами , , .

Решение: Площадь параллелограмма равна длине векторного произведения векторов, соответствующих двум соседним сторонам этого параллелограмма: . Длину векторов в декартовых координатах вычисляем по формуле: ; ; Подставляем в искомую формулу:

. Ответ: .

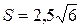Задача 1.11

Вычислить смешанное произведение , если , , .

Решение: Так как вектора заданы в декартовой системе координат, то можно воспользоваться формулой представления смешанного произведения через определитель 3-го порядка, а отсутствующие координаты в разложениях заменить нулем:

. Ответ: –25.

Задача 1.12

При каких значениях параметра (если таковые существуют) вектора и являются коллинеарными?

Решение: Два вектора коллинеарны, тогда и только тогда, когда их векторное произведение равно 0; нам известны координаты векторов в декартовой системе координат, поэтому распишем векторное произведение:

, которое должно быть равно нулю. Поэтому составляем следующее уравнение: . Вектор является базисным, поэтому он не может быть равным нулю, откуда: . Решая данное уравнение относительно параметра , получаем: . Ответ: при 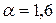векторы и коллинеарны.

Задача 1.13

При каком , если оно существует, векторы , и компланарны?

Решение: С одной стороны, вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю; с другой стороны можно расписать смешанное произведение через определитель 3-го порядка, откуда получаем: . Раскрываем определитель

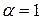. Это выражение должно быть равно нулю: . Решая данное уравнение относительно , получаем: . Ответ: при 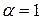исходные векторы компланарны.

Задача 1.14

Смешанное произведение . Найти смешанное произведение .

Решение: Согласно определению смешанного произведения:

{Используя свойства векторного произведения, имеем} 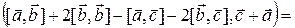{Так как , получаем} {По свойствам скалярного произведения}

{По определению смешанного произведения выражение преобразуется}

{В смешанном произведении неважен порядок векторного и скалярного произведения, поэтому выражение можно преобразовать}

{Так как , получаем} {Произведя циклическую перестановку членов смешанного произведения и учитывая знак, имеем}

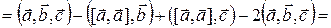{Используя тот факт, что , полчаем ответ} .

Ответ: .