Уравнение плоскости

Пусть в декартовой системе координат имеется некоторая плоскость, проходящая через точку , ее радиус-вектор будет иметь координаты . Зададим на этой же плоскости точку с радиус-вектором . Очевидно, что вектор также будет находиться в заданной плоскости (Рис. 2.6).

Рис. 2.6. Вектор на плоскости

Проведем перпендикуляр к плоскости . Скалярное произведение вектора с эти перпендикуляром будет равно 0: , или, в координатах:

.

(2.1)

Преобразуем данное уравнение: раскроем скобки и сгруппируем известные координаты: , обозначив , получим уравнение плоскости в общей форме:

,

(2.2)

где – координаты любой точки на плоскости; – координаты фиксированной точки на плоскости; – координаты нормали к плоскости. Если все коэффициенты общего уравнения не равны нулю, то уравнение (2.2) можно привести к виду:

.

(2.3)

Уравнение плоскости в данном виде называется уравнением плоскости в отрезках; в уравнении приняты обозначения: , , ; отрезки отсекаются плоскостью на осях координат.

Итак, плоскость в пространстве, как и прямая на плоскости, задается уравнением первой степени относительно координат. Поэтому говорят, что плоскость есть поверхность первого порядка.

Расстояние от точки до поверхности, заданной формулой (2.3) определяется по формуле:

,

(2.4)

Двугранный угол между плоскостями и совпадает с углом между их нормалями и вычисляется по формуле:

,

(2.5)

Для ортогональных плоскостей будет справедливо утверждение: или в координатной форме: .

Для параллельных плоскостей выполняется условие пропорциональности координат нормалей: . В частности, если, кроме того, выполняется условие , то плоскости совпадают.

Рассмотрим частные случаи расположения плоскости в декартовой системе координат.

1. : нормаль к плоскости параллельна оси . Поскольку для нормали имеем и уравнение (2.5) принимает вид: . В этом случае плоскость параллельна координатной оси .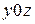

2. : проводя аналогичные рассуждения, получаем: , плоскость параллельная оси .

3. 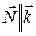: , плоскость параллельная оси .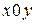

4. : вектор нормали лежит в плоскости 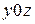, следовательно, плоскость параллельна оси . В этом случае , так как .

5. : , параллельна оси .

6. : 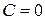, параллельна оси .

7. : это возможно лишь в случае, когда плоскость проходит через начало координат. При этом и плоскость задается уравнением , которому удовлетворяет точка .