Уравнение линии

Рассмотрим декартовую систему координат на плоскости.

Определение 2.1. Уравнение называется уравнением линии относительно заданной системы координат, если этому уравнению удовлетворяют координаты каждой точки, лежащей на этой линии, и не удовлетворяют координаты ни одной из точек, не лежащей на ней.

Линию еще называют кривой, а ее уравнение – уравнением в общем виде или в неявной форме.

Примеры линий

2.1. . Этому уравнению удовлетворяют точки, у которых абсцисса равна ординате, то есть данное уравнение описывает биссектрису I и III квадрантов (Рис. 2.1).

2.2. . Данное уравнение описывает биссектрису II и IV квадрантов (Рис. 2.1).

Рис. 2.1. Биссектрисы I и III квадрантов, II и IV квадрантов

2.3. . Этому уравнению удовлетворяют точки обеих биссектрис (и только они).

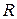2.4. Для точек, лежащих на окружности также можно записать уравнение в виде: , где – центр окружности, – радиус, 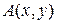- точка, принадлежащая окружности (2.2). Действительно, по определению окружность есть геометрическое место точек, равноудаленных от центра на расстояние 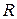. Вектор имеет координаты , значит, квадрат его длины равен .

Рис. 2.2. Окружность есть геометрическое место точек