 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Гипербола
|
|
Определение. Гиперболой называется геометрическое место точек плоскости, разность расстояний которых от двух данных точек, называемых фокусами, взятая по абсолютной величине, постоянна. Абсолютную величину этой разности принято обозначать 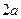 .
.
Каноническое уравнение гиперболы с центром в начале координат и полуосями действительной 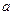 и мнимой
и мнимой  записывается в виде:
записывается в виде:
 .
.
 Гипербола имеет форму, изображенную на рис. 50. Точка
Гипербола имеет форму, изображенную на рис. 50. Точка 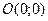 называется центром гиперболы, точки
называется центром гиперболы, точки  называются вершинами гиперболы,
называются вершинами гиперболы, 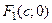 и
и  – фокусами гиперболы. Отрезки
– фокусами гиперболы. Отрезки 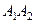 и
и 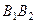 , а также их длины
, а также их длины 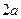 и
и  называются соответственно действительной и мнимой осями гиперболы. Числа
называются соответственно действительной и мнимой осями гиперболы. Числа 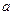 и
и  называются соответственно действительной и мнимой полуосями гиперболы. Длина отрезка
называются соответственно действительной и мнимой полуосями гиперболы. Длина отрезка 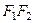 , равная
, равная  , называется фокусным расстоянием, а
, называется фокусным расстоянием, а  – полуфокусным расстоянием. Величины
– полуфокусным расстоянием. Величины 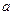 и
и  связаны соотношением
связаны соотношением  . Гипербола – кривая, симметричная относительно начала координат и координатных осей. В отличие от эллипса гипербола незамкнутая кривая, имеющая асимптоты – прямые, к которым ветви гиперболы неограниченно приближаются, не пересекая их и не касаясь. Уравнения асимптот
. Гипербола – кривая, симметричная относительно начала координат и координатных осей. В отличие от эллипса гипербола незамкнутая кривая, имеющая асимптоты – прямые, к которым ветви гиперболы неограниченно приближаются, не пересекая их и не касаясь. Уравнения асимптот
 и
и  .
.
 Каноническое уравнение гиперболы со смещенным центром:
Каноническое уравнение гиперболы со смещенным центром:
 .
.
Центр гиперболы находится в точке с координатами  .
.
Рассмотрим другие варианты уравнений гиперболы. Уравнение

является каноническим уравнением гиперболы с центром в начале координат и полуосями – действительной  и мнимой
и мнимой 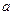 . Т.е. в этом случае вершины гиперболы
. Т.е. в этом случае вершины гиперболы  находятся на оси
находятся на оси 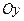 .
.
Гиперболы 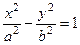 и
и  имеют общие асимптоты (рис. 51). Такие гиперболы называются сопряженными. На рис. 51 гипербола
имеют общие асимптоты (рис. 51). Такие гиперболы называются сопряженными. На рис. 51 гипербола  изображена пунктирной линией. Уравнение
изображена пунктирной линией. Уравнение  определяет гиперболу с центром в точке с координатами
определяет гиперболу с центром в точке с координатами  и полуосями – действительной
и полуосями – действительной  и мнимой
и мнимой 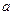 .
.
Определить какая ось действительная, а какая мнимая, легко по уравнению гиперболы, знак «+» перед квадратом переменной указывает на действительную ось, знак «–» указывает на мнимую ось.
Если в уравнении гиперболы  , гипербола называется равнобочной или равносторонней.
, гипербола называется равнобочной или равносторонней.
Чтобы построить гиперболу по её уравнению 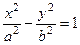 или
или  , надо:
, надо:
1 найти 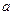 и
и  ,
,
2 на оси  в обе стороны от начала координат отложить отрезки длины
в обе стороны от начала координат отложить отрезки длины 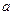 ,
,
3 на оси 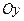 в обе стороны от начала координат отложить отрезки длины
в обе стороны от начала координат отложить отрезки длины  ,
,
4 построить основной прямоугольник, проведя через концы всех четырех отрезков прямые, параллельные осям координат,
5 построить асимптоты гиперболы, для этого в полученном основном прямоугольнике провести прямые, содержащие диагонали прямоугольника,
6 отметить вершины гиперболы – точки пересечения основного прямоугольника с действительной осью гиперболы,
7 построить гиперболу. (Если требуется более точный чертеж, можно найти из уравнения еще несколько точек гиперболы)
 Для построения гиперболы, заданной уравнением
Для построения гиперболы, заданной уравнением  или
или  , необходимо сначала нанести положение центра
, необходимо сначала нанести положение центра  на координатную плоскость, провести через центр оси симметрии
на координатную плоскость, провести через центр оси симметрии 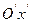 и
и 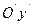 . Построить основной прямоугольник с центром в точке
. Построить основной прямоугольник с центром в точке  и сторонами
и сторонами 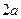 и
и  , провести диагонали прямоугольника, отметить вершины гиперболы на действительной оси и провести кривую (рис. 52).
, провести диагонали прямоугольника, отметить вершины гиперболы на действительной оси и провести кривую (рис. 52).
Определение. Эксцентриситетом гиперболы, так же как и эксцентриситетом эллипса называется отношение расстояния между фокусами к величине действительной оси:
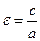 ,
,
здесь  – полуфокусное расстояние,
– полуфокусное расстояние, 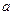 – действительная полуось.
– действительная полуось.
Для гиперболы  , так как
, так как  . С учетом
. С учетом  можно записать
можно записать
 .
.
Чем меньше эксцентриситет гиперболы, тем меньше отношение  , и тем больше вытянут её основной прямоугольник.
, и тем больше вытянут её основной прямоугольник.

Определение. Директрисами гиперболы называются прямые 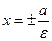 , где
, где 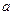 – действительная полуось (рис. 53). Директрисы гиперболы имеют то же свойство, что и директрисы эллипса. Если
– действительная полуось (рис. 53). Директрисы гиперболы имеют то же свойство, что и директрисы эллипса. Если 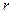 – расстояние от произвольной точки гиперболы до какого-нибудь фокуса,
– расстояние от произвольной точки гиперболы до какого-нибудь фокуса, 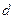 – расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение
– расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение 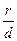 есть величина постоянная, равная эксцентриситету гиперболы
есть величина постоянная, равная эксцентриситету гиперболы 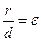 .
.
Дата публикования: 2015-07-22; Прочитано: 2533 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
