 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Окружность
|
|
Определение. Окружность есть геометрическое место точек плоскости, равноудаленных от данной точки – центра на данное расстояние – радиус.
Окружность определена, если заданы её центр и радиус.
Каноническое уравнение окружности с центром в точке 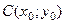 и радиусом
и радиусом  имеет вид:
имеет вид:
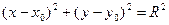 .
.
Полагая  , получим уравнение окружности с центром в начале координат:
, получим уравнение окружности с центром в начале координат:
 .
.
Эллипс
Определение. Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (её принято обозначать 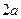 ).
).
Для того, чтобы получить ур-ие эллипса в простом виде ось ОХ направим через фокусы, а начало координат поместим в середине отрезка, соединяющего фокусы. Пусть М(х,у) – любая точка эллипса. По определению эллипса
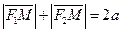
Обозначим расстояние между фокусами через  . Тогда фокусы будут иметь координаты
. Тогда фокусы будут иметь координаты 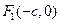 и
и  .
.
Длина первого вектора 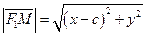
и второго 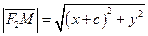 , т.о.
, т.о.

Возведем в квадрат 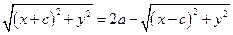 и получим
и получим
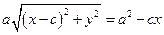
Еще раз возведем его в квадрат и получим
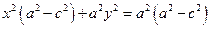
По свойству сторон треугольника 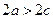

Обозначим  через
через 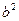 и разделим обе части последнего равенства на
и разделим обе части последнего равенства на 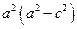 и получим
и получим
Каноническое уравнение эллипса с центром в начале координат и полуосями 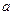 и
и 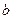
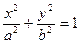
 Эллипс имеет форму, изображенную на рис. 47. Точка
Эллипс имеет форму, изображенную на рис. 47. Точка 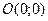 называется центром эллипса, точки
называется центром эллипса, точки 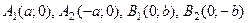 называются вершинами эллипса,
называются вершинами эллипса, 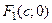 и
и  – фокусами эллипса. Отрезки
– фокусами эллипса. Отрезки 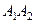 и
и 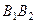 , а также их длины
, а также их длины 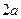 и
и  называются соответственно большой и малой осями эллипса, а числа
называются соответственно большой и малой осями эллипса, а числа 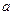 и
и 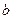 соответственно большой и малой полуосями эллипса. Длина отрезка
соответственно большой и малой полуосями эллипса. Длина отрезка 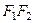 , равная
, равная  , называется фокусным расстоянием, а
, называется фокусным расстоянием, а  – полуфокусным расстоянием. Величины
– полуфокусным расстоянием. Величины 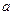 и
и 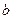 связаны соотношением
связаны соотношением 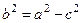 .
.
Если  , то уравнение
, то уравнение  определяет эллипс, большая ось которого
определяет эллипс, большая ось которого  лежит на оси
лежит на оси 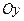 , а малая
, а малая 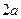 – на оси
– на оси  , фокусы такого эллипса находятся на оси
, фокусы такого эллипса находятся на оси 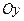 в точках
в точках 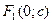 и
и 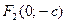 , а
, а 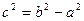 .
.
Каноническое уравнение эллипса со смещенным центром имеет вид:
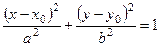 ,
,
центр эллипса находится в точке с координатами  рис. 48.
рис. 48.
 Чтобы построить эллипс по его уравнению
Чтобы построить эллипс по его уравнению  , надо:
, надо:
1. найти 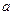 и
и 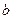 ,
,
2. на оси  в обе стороны от начала координат отложить отрезки длины
в обе стороны от начала координат отложить отрезки длины 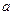 ,
,
3. на оси 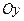 в обе стороны от начала координат отложить отрезки длины
в обе стороны от начала координат отложить отрезки длины 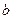 ,
,
4. через концы всех четырех отрезков провести прямые, параллельные осям координат (получили основной прямоугольник эллипса),
5. в полученный прямоугольник вписать эллипс. (Если требуется более точный чертеж, можно найти из уравнения еще несколько точек эллипса.)
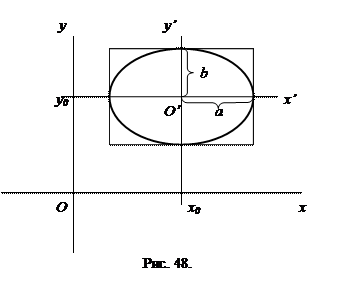
Для построения эллипса, заданного уравнением 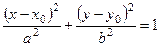 , необходимо сначала нанести положение центра
, необходимо сначала нанести положение центра  на координатную плоскость, провести через центр эллипса оси симметрии
на координатную плоскость, провести через центр эллипса оси симметрии 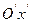 и
и 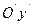 , построить основной прямоугольник с центром в точке
, построить основной прямоугольник с центром в точке  со сторонами
со сторонами 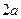 и
и  , вписать в него эллипс (рис. 48).
, вписать в него эллипс (рис. 48).
Определение. Отношение 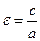 называется эксцентриситетом эллипса и характеризует форму (степень сжатия) эллипса.
называется эксцентриситетом эллипса и характеризует форму (степень сжатия) эллипса.
Для эллипса 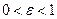 , так как
, так как  . С учетом
. С учетом 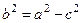 можно записать
можно записать
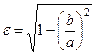 .
.
Чем больше эксцентриситет, тем больше эллипс отличается от окружности (более «сплющен»).

Определение. Директрисами эллипса называются прямые 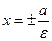 , где
, где 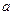 – большая полуось (рис. 49).
– большая полуось (рис. 49).
Свойство директрис состоит в следующем. Если 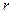 – расстояние от произвольной точки эллипса до какого-нибудь фокуса,
– расстояние от произвольной точки эллипса до какого-нибудь фокуса, 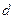 – расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение
– расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение 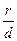 есть величина постоянная, равная эксцентриситету эллипса
есть величина постоянная, равная эксцентриситету эллипса 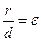 .
.
Дата публикования: 2015-07-22; Прочитано: 565 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
