 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Переход от полярных координат точки к декартовым, и обратно
|
|
Пусть точка M(r,φ) задана в полярной системе координат.

Рис.3
Совместим полярную и декартову системы координат так, чтобы ось полярной системы совпала с осью ОХ, а полюс с началом координат (Рис.3). Тогда каждой точке M(r,φ) в полярной системе координат будет соответствовать единственная точка M(x,y), координаты которой, как видно из Рис.3, вычисляются по формулам:
 ( 1.3 )
( 1.3 )
Это и есть формулы перехода от полярных координат точки к декартовым.
Формулы перехода от декартовых координат точки к полярным следуют из формул (1.3):
 (1.4)
(1.4)
1.1. Примеры решения задач.
В полярной системе координат построить точки 
Рассмотрим примеры решения задач 1-го типа:
Какие линии заданы следующими уравнениями?
1.  - ось ОХ
- ось ОХ
2.  - биссектриса 1-го и 3-го коорд. угла
- биссектриса 1-го и 3-го коорд. угла
3.  - две прямые
- две прямые
4.  -окружность с С(0,0)
-окружность с С(0,0)
5.  С(0,0)
С(0,0)
6.  - не имеет геометрического образа на пл-ти
- не имеет геометрического образа на пл-ти
7.  - ур-ие окружности
- ур-ие окружности
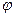
| 
| 
| 
| 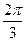
| 
| |
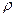
| 
| 
| 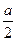
| 
| 
|
Дата публикования: 2015-07-22; Прочитано: 5333 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
