Перпендикулярно данному вектору

Найдём уравнение прямой, проходящей через заданную точку М₀ (х₀,у₀) перпендикулярно данному вектору 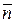(А,В).

Возьмём на прямой произвольную точку М (х,у) и рассмотрим вектор М₀М = (х – х₀, у – у₀) (см. рис. 3.17).

Рис. 3.17.

Поскольку векторы 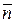и М₀М перпендикулярны, то их скалярное произведение равно нулю: 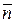∙ М₀М = 0, то есть

А (х – х₀) + В (у – у₀) = 0. (3.45)

Уравнение (3.45) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.

Вектор 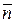(А,В), перпендикулярный прямой, называется нормальным вектором этой прямой.