Задачи для самостоятельного решения. 2.Имеются пять ключей, из которых только один подходит к замку

1. Пусть Х – выручка фирмы в долларах. Найдите распределение выручки в рублях Z = XY в пересчете по курсу доллара Y, если выручка Х не зависит от курса Y, а распределения Х и Y имеют вид:

X:

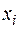
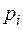
	0,7	0,3

Y:

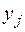
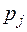
	0,4	0,6

2. Имеются пять ключей, из которых только один подходит к замку. Найдите закон распределения случайной величины Х, равной числу проб при открывании замка, если испробованный ключ в последующих попытках не участвует.

3. На пути движения автомобиля шесть светофоров, каждый из которых разрешает или запрещает дальнейшее движение с вероятностью 0,5. Найдите закон распределения случайной величины Х, равной числу светофоров, пройденных автомобилем до первой остановки или до прибытия к месту назначения.

4. В партии из десяти деталей имеется восемь стандартных. Из этой партии наугад взято две детали. Найдите закон распределения случайной величины Х – числа стандартных деталей в выборке.

5. Напишите закон распределения дискретной случайной величины Х – числа появлений «герба» при трех бросаниях монеты.

6. Дискретная случайная величина Х – число мальчиков в семье из пяти детей. Предполагая равновероятными рождение девочки и мальчика: а) найдите закон распределения случайной величины Х; б) постройте многоугольник распределения Х; в) найдите вероятности событий А:{в семье не менее двух, но не более трех мальчиков}, В:{в семье не более трех мальчиков} и С:{в семье не более одного мальчика}.

7. В партии 10 % нестандартных деталей. Наугад отобраны четыре детали. Составьте закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырех отобранных и постройте многоугольник полученного распределения.

8. Рабочий обслуживает четыре независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна: для первого станка 0,7, для второго – 0,75, для третьего – 0,8, для четвертого – 0,9. Найдите закон распределения случайной величины Х – числа станков, которые не потребуют внимания рабочего.

9. Устройство состоит из трех элементов, работающих независимо друг от друга. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составьте закон распределения числа отказавших элементов в одном опыте.

10. Вероятность того, что стрелок попадает в мишень при одном выстреле, равна 0,8. Стрелку последовательно выдаются патроны до тех пор, пока он не промахнется (число патронов не ограниченно). Требуется: а) составить закон распределения дискретной случайной величины Х – числа патронов, выданных стрелку; б) построить многоугольник полученного распределения.

11. АТС обслуживает 1500 абонентов. Вероятность того, что в течение 3 минут на АТС поступит вызов, равна 0,002. Постройте ряд распределения с. в. X, равной числу вызовов, поступивших на АТС в течение 3 минут. Найдите вероятность того, что за это время поступит более трех вызовов.

12. С вероятностью попадания при одном выстреле 0,7 охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Требуется: а) найти закон распределения Х; б) построить многоугольник распределения.

13. Две игральные кости одновременно бросают два раза. Напишите закон распределения дискретной случайной величины Х – числа выпадений четного числа очков на двух игральных костях.

14. Даны законы распределения двух независимых случайных величин:

X:

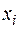
	–3
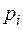
	0,3	0,5	0,2

Y:

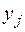
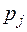
	0,4	0,6

Найдите закон распределения случайных величин: а) Z = X + Y;

б) Z = XY; в) ;г) .

15. В партии из 25 курток пять имеют скрытый дефект. Покупают три куртки. Найдите закон распределения числа дефектных курток среди купленных. Постройте многоугольник распределения.

16. Из партии в 20 изделий, среди которых имеется шесть бракованных, выбраны случайным образом три изделия для проверки на качество. Постройте ряд распределения случайного числа Х хороших изделий среди отобранных.

17. В коробке 20 одинаковых катушек ниток, из них – четыре катушки с белыми нитками. Наугад вынимают две катушки. Найдите закон распределения числа катушек с белыми нитками среди вынутых.

18. Баскетболист делает три штрафных броска. Вероятность попадания при каждом броске равна 0,7. Постройте ряд распределения числа попаданий мяча в корзину.

19. Имеются три базы с независимым снабжением. Вероятность отсутствия на базе нужного товара равна 0,1. Предприниматель решил закупить некий товар. Составьте закон распределения числа баз, на которых в данный момент этот товар находится.

20. Бросают три игральных кубика. Составьте закон распределения числа выпавших «шестерок» на трех кубиках. Постройте многоугольник распределения.

21. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента равна 0,15. Составьте закон распределения отказавших элементов.

22. Абитуриент должен сдать три экзамена. Вероятность успешной сдачи первого экзамена равна 0,8, второго – 0,7, третьего – 0,7. Постройте ряд распределения числа экзаменов, сданных абитуриентом.

23. Вероятность того, что аудитор допустит ошибку при проверке бухгалтерского баланса, равна 0,05. Аудитору на заключение представлено два баланса. Составьте закон распределения числа правильных заключений на проверяемые балансы.

24. Вероятность сбоя в работе АТС равна 0,1. Составьте закон распределения числа сбоев, если в данный момент поступило пять вызовов.

25. Вероятность того, что автомат при опускании одной монеты срабатывает правильно, равна 0,98. Постройте ряд распределения случайной величины – числа опусканий монет в автомат до первого правильного срабатывания автомата. Найдите вероятность того, что будет опущено пять монет.

26. В магазин привезли арбузы из Ташкента и Камышина в равных количествах. Вероятность покупки неспелого арбуза равна соответственно 0,1 и 0,3. Куплено четыре арбуза. Составьте закон распределения спелых арбузов среди купленных.

27. У продавца имеются изделия, полученные в равных количествах с трех фабрик. Вероятность того, что эти изделия отличного качества, для каждой фабрики соответственно равны 0,8; 0,7 и 0,9. Отобрано два изделия. Составьте закон распределения количества изделий отличного качества среди отобранных.

28. В лотерее 100 билетов, из которых два выигрышных по 50 руб. и 10 выигрышных по 1 руб. стоимость билета 2 руб. Составьте закон распределения суммы чистого выигрыша для лица, купившего два билета. Постройте многоугольник распределения.

29. Среди 15 собранных агрегатов шесть нуждаются в дополнительной смазке. Составьте закон распределения числа агрегатов, нуждающихся в дополнительной смазке, среди пяти наугад отобранных из общего числа.

3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

Закон распределения полностью характеризует случайную величину. Однако при решении многих практических задач достаточно знать лишь некоторые числовые параметры, характеризующие отдельные существенные свойства закона распределения. Такие числа принято называть числовыми характеристиками случайных величин.

К числовым характеристикам случайной величины относят: математическое ожидание (центр распределения с. в.), моду, медиану, дисперсию (отклонение значений с. в. от ее центра) и среднее квадратическое отклонение.

Пусть д. с. в. задана законом распределения:

			…
			…

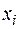
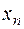
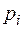
Математическим ожиданием (илисреднимзначением)д. с. в. 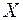называют сумму произведений возможных значений случайной величины на соответствующие им вероятности, то есть:

.

Математическое ожидание обладает следующими свойствами:

1. Математическое ожидание постоянной величины равно самой постоянной, то есть, справедлива формула:

.

Следствие: .

2. Постоянный множитель можно вынести за знак математического ожидания, то есть .

Следствие: .

3. Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих величин:

.

4. Для независимых случайных величин:

.

Дисперсией (рассеиванием)д. с. в. называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, то есть:

.

Или проще, дисперсия д. с. в. равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

,

где .

Дисперсия обладает следующими свойствами:

1.Дисперсия постоянной величины равна 0, то есть .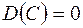

Следствие: .

2.Постоянный множитель выносят из-под знака дисперсии в квадрате, то есть .

Следствие: .

3.Дисперсия суммы двух независимых случайных величин Х и Y равна сумме их дисперсий, то есть .

4. Если случайные величины Х и Y независимы, то

.

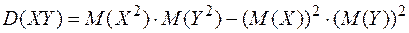Справедливы следующие формулы для 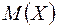, 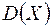некоторых распределений:

– Биномиальное распределение: .

– Распределение Пуассона: .

– Геометрическое распределение если оно бесконечно убывающее: .

– Гипергеометрическое распределение:

.

Дисперсия имеет размерность квадрата с. в. Х, что в сравнительных целях неудобно. Если желательно, чтобы оценка разброса (рассеивания) имела размерность с. в., используют среднее квадратическое отклонение.

Средним квадратическим отклонением 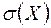случайной величины Х называется квадратный корень из дисперсии, то есть

.

Функцией распределения случайной величины Х называется функция 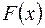, выражающая для каждого х вероятность того, что с. в. Х примет значение, меньшее х:

.

Так как до значения случайная величина Х не встречалась, то и вероятность события равна нулю. Для всех значений вероятность события совпадает с вероятностью значения , то есть р ₁ и т.д. имеем:

Графически функция распределения выглядит как показано рис. 3.

Рис. 3. Функция распределения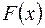

Функцию 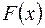также называют интегральной функцией распределения. Она дает общий способ задания как дискретных, так и непрерывных случайных величин.

Свойства интегральной функции распределения:

1. ограничена, то есть .

2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси.

3. .

4. Вероятность попадания случайной величины в промежуток равна: (рис. 3).

5. 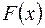непрерывна слева, то есть

.

Модой М₀ дискретной случайной величины Х называется ее значение, принимаемое с наибольшей вероятностью в ряде распределения.

Математическое ожидание и дисперсия являются частными случаями более общих понятий – моментов случайных величин.

Начальным моментом порядка k случайной величины X называется математическое ожидание k- ой степени этой величины, обозначается через , то есть вычисляется по формуле:

.

В частности, начальный момент первого порядка равен математическому ожиданию: .

Центральным моментом порядка k случайной величины X называется математическое ожидание величины , обозначается через и справедлива формула:

.

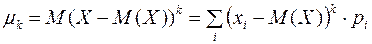В частности, центральный момент первого порядка равен 0, то есть центральный момент второго порядка равен дисперсии: .

Центральные моменты могут быть выражены через начальные моменты. Так,

.

Примеры:

1. Дискретная случайная величина задана законом распределения:

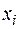
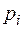
	0,2	0,4	0,3	0,1

Требуется вычислить: а) математическое ожидание ;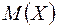

б) дисперсию 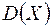; в) среднее квадратическое отклонение ;

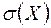г) начальные и центральные моменты 1-го и 2-го порядков.

Решение.

а) Математическое ожидание вычислим по формуле:

.

;

б) дисперсию вычислим по формуле:

. (*)

Вычислим все возможные значения квадрата отклонения:

,

,

,

.

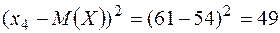Чтобы вычислить дисперсию 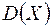, составим закон распределения квадрата отклонения и затем применим формулу (*):

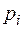
	0,2	0,4	0,3	0,1

.

Можно вычислить дисперсию проще по формуле :

	482	532	572	612
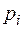
	0,2	0,4	0,3	0,1

;

в) среднее квадратическое отклонение вычислим по формуле , получим ;

г) начальный момент первого порядка: .

Найдем начальный момент второго порядка по формуле , получим .

Центральные моменты будут равны:

2. Из 25 контрольных работ, среди которых пять оценены на «отлично», наугад извлекают три работы. Составьте закон распределения числа работ, оцененных на «отлично» среди отобранных. Найдите функцию распределения 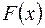случайной величины и постройте ее график. Найдите для Х моду М ₀.

Решение. Так как выбирают три работы, то случайная величина Х может принимать значения 0; 1; 2; 3. Найдем вероятности этих значений:

,

,

,

.

Искомый закон распределения:

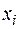
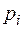
	0,496	0,413	0,087	0,004

Функцию распределения 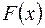найдем по формуле :

График представлен на рис. 4:

Рис. 4. Функция распределения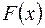

Моду найдем по максимальной вероятности в ряде распределения: .

3. Функция распределения с. в. Х имеет вид:

.

Найдите вероятность того, что случайная величина принимает значение в интервале [1; 3).

Решение.

По формуле имеем:

.

4. Даны законы распределения двух случайных величин Х и Y:

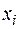
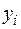
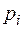
		0,3	0,7		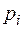	0,5	0,2	0,3

Найдите:

а) числовые характеристики , , , , , ;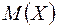

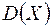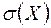б) ;

в) , составив закон распределения с. в. .

Решение.

а) Математическое ожидание вычислим по формуле:

.

.

Дисперсию вычислим по формуле :

.

Среднее квадратическое отклонение вычислим по формуле , получим .

Аналогично вычисляем для д. с. в. :

;

б) используя свойства математического ожидания и дисперсии, получим:

,

,

;

в) составим закон распределения для .

	Y
Х		0,5	0,2	0,3
	0,3	2∙10+30=50	2∙10+40=60	2∙10+60=80
	0,7	2∙20+30=70	2∙20+40=80	2∙20+60=100

Итак, с. в. Z может принимать значения:

. Вероятности соответственно будут равны:

,

,

Тогда закон распределения с. в. Z имеет вид:

	0,15	0,06	0,35	0,23	0,21

(Контроль ).

.

5. Даны значения случайной величины: 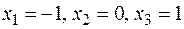и , . Найдите .

Решение. Составим систему из условий:

Тогда

или

; .