Пример. Торговая база получила 1000 электролампочек

Торговая база получила 1000 электролампочек. Вероятность повреждения электролампочки в пути 0,001. Составьте закон распределения поврежденных электролампочек, указав первые пять значений этой случайной величины. Определите вероятность того, что в пути было повреждено четыре электролампочки.

Решение. Пусть случайная величина X – количество поврежденных электролампочек. Данная с. в. может принимать множество значений 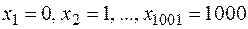. Отсюда 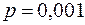следовательно, имеем дело с редкими событиями и 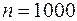– достаточно велико, поэтому для решения задачи используем формулу Пуассона:

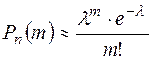, где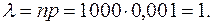

Тогда вероятности значений с. в. будут равны:

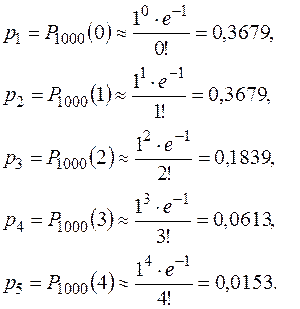
Искомое распределение примет вид:

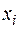
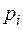
	0,3679	0,3679	0,1839	0,0613	0,0153

Проверку сделать в данном примере достаточно сложно, так как случайная величина имеет большое количество значений.

Вероятность того, что в пути было повреждено четыре лампочки, будет равна:

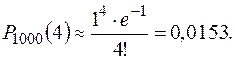
Геометрическое распределение. Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р, следовательно, вероятность его непоявления 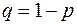. Испытания заканчиваются, как только появляется событие А.

Пусть в первых 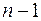испытаниях событие А не появилось, а в п -ом испытании появилось. Тогда 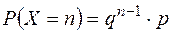. Полагая, 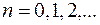получим геометрическую прогрессию:

.

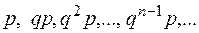Случайную величину, распределенную по геометрическому закону, можно интерпретировать как число 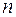опытов (испытаний), проведенных по схеме Бернулли до первого положительного исхода.