Числовые характеристики непрерывной случайной величины

Математическим ожиданием или средним значением н. с. в. Х с плотностью распределения , называется число

.

Если возможные значения н. с. в. принадлежат промежутку , то

.

Дисперсией н. с. в. Х с плотностью распределения называется значение интеграла

или .

Если возможные значения н. с. в. принадлежат промежутку , то

или .

Средним квадратическим отклонением называется величина

.

Начальным моментом порядка k непрерывной случайной величины X называется математическое ожидание k- ой степени этой величины, обозначается через , то есть вычисляется по формуле:

.

Центральным моментом порядка k непрерывной случайной величины X называется математическое ожидание величины , обозначается через и справедлива формула:

.

Так же как и для дискретных случайных величин, центральные моменты могут быть выражены через начальные моменты:

.

Среди моментов высших порядков особое значение имеют центральные моменты третьего и четвертого порядков, называемых соответственно коэффициентами асимметрии эксцесса.

Коэффициентом асимметрии («скошенности») А случайной величины называется величина:

.

Коэффициентом эксцесса («островершинности») Е случайной величины называется величина:

.

Модой н. с. в. Х с плотностью распределения называется такое значение этой величины, при котором функция достигает максимума.

Медианой н. с. в. Х называется такое ее значение, которое определяется равенством .

Квантилью порядка р н. с. в. называется ее значение , являющиеся корнем уравнения . Таким образом, является решением уравнения .

Квантиль порядка 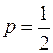называется медианой.

Примеры:

1. Найдите математическое ожидание и дисперсию с. в. Х, заданной функцией распределения

Решение. Найдем :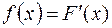

Тогда .

.

2. С. в. Х задана функцией плотности вероятностей

Найдите ее числовые характеристики: математическое ожидание, дисперсию, среднеквадратическое отклонение, моду, медиану, асимметрию и эксцесс.

Решение. Найдем математическое ожидание:

.

Теперь вычислим дисперсию и среднеквадратическое отклонение:

.

Мода есть максимум функции плотности распределения вероятностей, то есть .

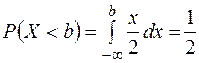Медиану найдем из условия , т.е. , откуда .

Наконец, вычислим асимметрию:

и эксцесс:

.