Задачи для самостоятельного решения. 1. Случайная величина Х задана плотностью вероятности в интервале (0; 4), вне этого интервала

1. Случайная величина Х задана плотностью вероятности в интервале (0; 4), вне этого интервала . Найдите математическое ожидание, дисперсию, среднеквадратическое отклонение величины Х.

2. Случайная величина Х задана плотностью вероятности в интервале (0; 1). Вне этого интервала . Найдите параметр С и числовые характеристики величины Х.

3. Случайная величина Х задана плотностью вероятности в интервале (3; 5), вне этого интервала . Найдите моду, медиану и математическое ожидание величины Х.

4. Случайная величина Х задана плотностью вероятности в интервале (2; 4), вне этого интервала . Найдите моду, медиану и математическое ожидание величины Х.

5. Случайная величина Х задана в интервале (0; π) плотностью вероятности , вне этого интервала . Найдите дисперсию величины Х.

6. Случайная величина Х задана плотностью вероятности в интервале , вне этого интервала . Найдите математическое ожидание и дисперсию величины Х.

7. Найдите математическое ожидание случайной величины Х, заданной функцией распределения

8. Найдите дисперсию с. в. Х:

9. Дана функция

Найдите параметр С, числовые характеристики случайной величины Х.

10. С. в. Х задана функцией распределения

Найдите: а) плотность вероятности ; б) числовые характеристики с. в. Х; в) ; в) постройте графики и .

11. Непрерывная случайная величина Х распределена в интервале (0; 1) по закону с плотностью вероятности Найдите математическое ожидание и дисперсию случайной величины .

6. ВАЖНЕЙШИЕ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. «ПРАВИЛО ТРЕХ СИГМ»

Для непрерывной случайной величины выделяют равномерное, показательное и нормальноераспределения.

1.Н. с. в. Х имеет равномерное распределение на отрезке [ a; b ], если на этом отрезке плотность распределения вероятности с. в. постоянна, а вне его равна нулю, то есть

Функция распределения имеет вид:

Графики плотности и функции распределения для равномерного распределения представлены на рис. 8.

			y =0

Рис. 8. и для равномерного распределения

Вероятность попадания равномерно распределенной с. в. Х в интервале равна:

.

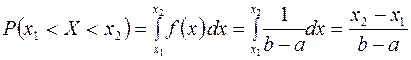Математическое ожидание .

Дисперсия .

К случайным величинам, имеющим равномерное распределение, относятся: время ожидания пассажиром транспорта, курсирующего с определенным интервалом; ошибка округления числа до целого (она равномерно распределена на [–0,5; 0,5]), и вообще случайные величины, о которых известно, что все их значения лежат внутри некоторого интервала, и все они имеют одинаковую вероятность (плотность).

2.Непрерывная с. в. Х распределена по показательному закону, если ее плотность вероятности имеет вид:

где – параметр показательного распределения. Функция распределения имеет вид:

Графики плотности и функции распределения для показательного распределения представлены на рис. 9.

x

Рис. 9. и для показательного распределения

Вероятность попадания случайной величины , распределенной по показательному закону, в интервале :

.

Математическое ожидание и дисперсия для показательного распределения:

.

Показательное распределение используется в приложениях теории вероятностей, особенно в теории массового обслуживания, в физике, в теории надежности. Оно используется для описания распределения случайной величины вида: длительность работы прибора до первого отказа, длительность времени обслуживания в системе массового обслуживания и т.д.

3. Нормальное распределение (распределение Гаусса) – это распределение н. с. в. Х, характеризуемое плотностью вероятности:

,

где – математическое ожидание;

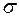– среднее квадратическое отклонение с. в. Х.

Тот факт, что с. в. Х имеет нормальное распределение с параметрами и 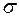, сокращенно записывается так: ~ .

Функция распределения имеет вид:

,

где 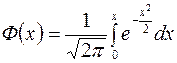– функция Лапласа.

Графики плотности и функции распределения для нормального распределения представлены на рис. 10.

Рис. 10. и для нормального распределения

Вероятность того, что с. в. Х примет значение, принадлежащее интервалу 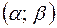равна:

.

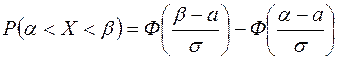Мода и медиана для нормально распределенной с. в. Х будут равны: .

Коэффициенты асимметрии и эксцесса равны: и .

Нормальному закону подчиняются ошибки измерений, величины износа деталей в механизмах, рост человека, ошибки при стрельбе, величина шума в радиоприемном устройстве и т.д.

Вероятность того, что с. в. Х, распределенная по нормальному закону, отклонится от своего математического ожидания на величину, меньшую положительного числа 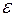равна:

.

Пологая в равенстве , получим:

,

то есть отклонение с. в. Х от своего математического ожидания меньше, чем на – почти достоверное событие.

Получаем известное «правило трех сигм», которое утверждает, что нормально распределенная с. в. Х практически не принимает значений вне интервала .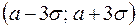

Примеры:

1. Поезда данного маршрута городского трамвая идут с интервалом 5 мин. Пассажир подходит к остановке в произвольный момент времени. Какова вероятность появления пассажира не ранее чем через минуту после ухода предыдущего вагона, но не позднее чем за две минуты до отхода следующего поезда? Найдите .

Решение. Время ожидания поезда есть с. в. Х, имеющая равномерное распределение вероятностей. Из условия задачи ; . Тогда, применяя формулу получим:

Тогда .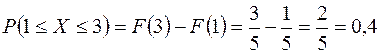

; ;

.

2. Время t расформирования состава через горку – случайная величина, подчиненная показательному закону. Пусть – среднее число поездов, которые горка может расформировать за 1 час. Определите вероятность того, что время расформирования состава больше 6 мин., но не меньше 24 мин. Найдите .

Решение. Используя формулу , находим: .

.

3. Случайная величина Х – время работы электролампочки имеет показательное распределение. Определите вероятность того, что время работы лампочки будет не меньше 600 часов, если среднее время работы 400 часов.

Решение. По условию задачи математическое ожидание с. в. Х равно 400 часов, следовательно, (так как ). Искомая вероятность , где и . Окончательно, .

4. Цена деления шкалы амперметра равна 0,1 А. Показания амперметра округляют до ближайшего целого деления. Найдите вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А.

Решение. Ошибку округления отсчета можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними целыми делениями. Плотность равномерного распределения , где – длина интервала, в котором заключены возможные значения Х; вне этого интервала . В рассматриваемой задаче длина интервала, в котором заключены возможные значения Х, равна 0,1, поэтому . Легко сообразить, что ошибка отсчета превысит 0,02, если она будет заключена в интервале (0,02; 0,08).

По формуле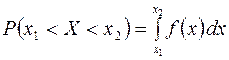

имеем:

.

5. Случайная величина Х распределена по нормальному закону. Математическое ожидание ; дисперсия . Найдите вероятность того, что в результате испытания Х примет значение в интервале (4; 7).

Решение.

По условию задачи имеем: . Подставив эти данные в формулу

,

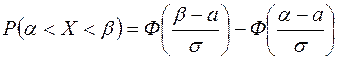имеем:

.

6. Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Стандартная длина (математическое ожидание) см, среднее квадратическое отклонение см. Найдите вероятность того, что отклонение длины от стандартной составит по абсолютной величине не более 0,6 см.

Решение. Если Х – длина детали, то по условию задачи эта величина должна быть в интервале , где . Используем формулу:

.

Подставив данные получим:

.

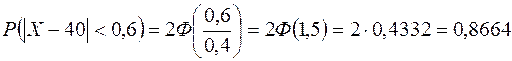Следовательно, вероятность того, что изготавливаемые детали по длине будут в пределах от 39,4 до 40,6 см, составляет 0,8864.

7. Диаметр деталей, изготовленных заводом, является случайной величиной, распределенной по нормальному закону. Стандартная длина диаметра см, среднее квадратическое отклонение . В каких границах можно практически гарантировать длину диаметра этой детали, если за достоверное принимается событие, вероятность которого равна 0,9973.

Решение.

По условию задачи имеем:

.

Применяя формулу , получим равенство:

или . По табл. А.2 находим, что такое значение функция Лапласа имеет при х =3. Следовательно ; откуда . Таким образом, можно гарантировать, что длина диаметра будет изменяться в пределах от 2,47 до 2,53 см.

8. Случайные значения веса зерна распределены нормально. Математическое ожидание веса зерна равно 0,15 г, среднее квадратическое отклонение равно 0,03 г. Нормальные всходы дают зерно, вес которых более 0,1 г. Определите: а) процент семян, от которых следует ожидать нормальные всходы; б) величину, которую не превзойдет вес отдельного зерна с вероятностью 0,99.

Решение.

Пусть с. в. Х – вес зерна. По условию .

а) Процент семян, дающих нормальные всходы – это вероятность получить нормальный всход от взятого наугад зерна. По условию нормальный всход бывает у зерен, вес которых более 0,1 г. Следовательно, те зерна, вес которых удовлетворяет условию , дают нормальные всходы. Определяем вероятность этого события.

Таким образом, от 95,2 % следует ожидать нормального всхода;

б) обозначим искомую величину через 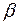. Находим ее из условия или . Выражение для вероятности в левой части запишем через функцию Лапласа:

Отсюда находим значение функции Лапласа: . По табл. А.2 находим значение аргумента для значения функции 0,49; оно равно 2,33, тогда , отсюда .

Таким образом, вес взятого зерна не будет превышать 0,22 г с вероятностью 0,99.

9. Масса вагона – с. в. Х, подчиненная нормальному закону распределения с математическим ожиданием т, средним квадратическим отклонением т. Покажите выполнение «правила трех сигм».

Решение.

Для подтверждения правила трех сигм сначала найдем границы отклонения .

; .

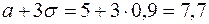Вероятность попадания с. в. Х в интервал (2,3; 7,7) равна:

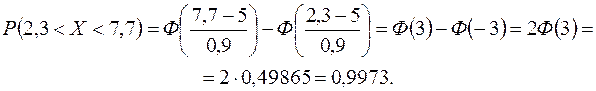
Значит, правило трех сигм выполняется.