Способы задания последовательностей

Последовательности задаются несколькими способами: аналитическим (формульным), словесным, графическим.

Аналитический способ: указывается формула, связывающая значение -ого члена последовательности с его номером . Зная ее, мы можем получить любой член последовательности.

Пример 25.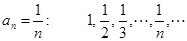

Пример 26.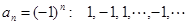

Пример 27.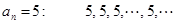

Определение 21. Последовательность, общий член которой не зависит от , называется постоянной (см. Пример 27).

Используется также рекуррентный способ: задаются несколько первых членов последовательности и формула, называемая рекуррентным соотношением, выражающая следующие члены последовательности через предыдущие, например: 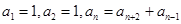при 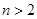(это последовательность Фибоначчи).

Словесный способ: закон соответствия между номером члена и значением этого члена может быть задан словесно.

Пример 28. Каждому натуральному числу сопоставляется число, равное -ому десятичному знаку после запятой числа 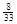в десятичной записи. Этот закон определяет последовательность, у которой ;…

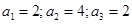Пример 29. Последовательность всех простых чисел 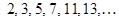Мы можем найти любой член этой последовательности, однако нет формулы для -го простого числа, и нет формулы, выражающей -ое простое число через предыдущие.

Графический способ: используются две интерпретации - двумерная (на плоскости) и одномерная (на числовой прямой).

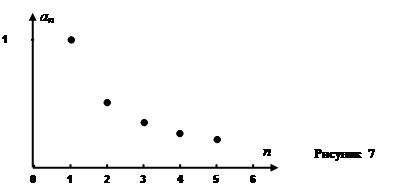Так как последовательность 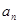является функцией, то геометрически эту функцию можно изобразить с помощью ее графика, то есть множества точек 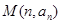координатной плоскости. Например, .

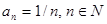Члены последовательности изображаются также точками координатной прямой. Например, .

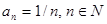Примечание: по известным первым членам последовательности, если нет никаких других указаний, невозможно указать закон ее образования. Так, четыре первые члена некоторой последовательности: могут быть, например, началом последовательности нечетных чисел или последовательности с формулой общего члена .

Для каждой последовательности должен быть задан закон, по которому мы можем получить любой ее член. В каком виде задан этот закон – не имеет значения.