Степенные ряды

Частным случаем функциональных рядов являются степенные ряды, имеющие вид

,

где а _n – действительные числа, называемые коэффициентами ряда, n =0, 1, 2, …, а число х ₀ называется центром степенного ряда. Таким образом, членами степенных рядов являются степенные функции.

Существует число r, 0 £ r £ ¥, называемое радиусом сходимости степенного ряда такое, что при | x – x₀ | < r ряд сходится, а при | x – x₀ | > r – расходится. При x=x₀+r и x=x₀ – r степенной ряд может как сходиться, так и расходиться. n

Интервал (x₀ – r, x₀ + r) называется интервалом сходимости степенного ряда.

Радиус сходимости степенного ряда может быть вычислен по формуле: если , то . При этом считается, что при q = 0 r = ¥, а при q = ¥ r = 0.n

Пример 3.10.

Ряд имеет радиус сходимости r=1, поскольку .

Ряд имеет радиус сходимости r=¥, поскольку .

Ряд расходится в граничных точках x = x₀ +1 и x = x₀ – 1 интервала сходимости.

Ряд имеет радиус сходимости r=1, поскольку ; в граничной точке x = x₀ + 1 он расходится (гармонический ряд), а в граничной точке x = x₀ – 1 сходится (признак Лейбница).

Ряд имеет радиус сходимости r = 1, поскольку ; в обеих граничных точках интервала сходимости х = х₀ ± 1 этот ряд сходится абсолютно. n

В каждой внутренней точке интервала сходимости степенной ряд сходится абсолютно. Во всяком замкнутом промежутке, который целиком лежит в интервале сходимости, степенной ряд сходится равномерно. n

Если два степенных ряда и 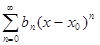имеют один и тот же интервал сходимости и во всех его точках имеют одинаковые суммы, то эти ряды совпадают, т.е. а_n = b_n, , n = 0, 1,2. … n

Сумма s(x) степенного ряда, , для всех значений х из интервала сходимости (x₀ – r, x₀ + r) есть непрерывная функция. n

Степенной ряд всегда можно почленно интегрировать на любом отрезке [ x₁, x₂ ] из интервала сходимости [ x₁, x₂ ] Ì (x₀ – r, x₀ + r):

n

Степенной ряд внутри его интервала сходимости можно дифференцировать почленно любое число раз:

n

Ряд Тейлора. Если действительная функция f(x) определена в некоторой окрестности точки х₀ и имеет в этой точке производные всех порядков, то ее рядом Тейлора называется степенной ряд, коэффициенты которого имеют вид a_n = , т.е.

.

Если функция f(x) представима в некоторой окрестности заданной точки х₀ степенным рядом, т.е. представима в виде в этой окрестности, то такой ряд единствен и является ее рядом Тейлора в точке х₀, т.е. n

Если на интервале (x₀ – h, x₀ + h) все производные заданной функции f(x) ограничены по совокупности, т.е. если существует число А > 0 такое, что | f⁽ⁿ⁾(x) | £ A для всех n = 0, 1, 2, … и х Î (x₀ – h, x₀ + h), то записанный в этой точке ряд Тейлора сходится к f(x) для всех х, таких что | x – x₀ | < h, т.е. имеет место формула 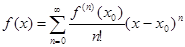n

Ряд Маклорена. Он получается из ряда Тейлора, если в качестве центра степенного ряда взять х₀ = 0, т.е. ряд Маклорена для функции, имеющей в точке х₀ = 0 производные всех порядков, имеет вид:

.

Пример 3.11.

Для |x| £ 1 функция arctg x разлагается в ряд Маклорена

,

откуда при х = 1 получаем

.

Для –1 < x £ 1 функция ln (1+x) разлагается в ряд Маклорена

,

откуда при х = 1 получаем

.

Для любого действительного х функция разлагается в ряд Маклорена

,

после чего эта функция легко интегрируется как ряд, почленно; дело в том, что интеграл

не берется в квадратурах, но с помощью ряда Маклорена получаем для любого х:

n