Функциональные ряды

Функциональный ряд 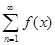называется сходящимся на множестве X, xÎX, если при любом фиксированном x₀ Î X сходится числовой ряд 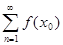, т.е. если при любом фиксированном x₀ Î X существует конечный предел 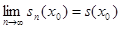. В этом случае определена функция s(x) на множестве Х, которая называется суммой функционального ряда

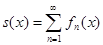
Множество Х, в каждой точке которого ряд 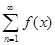сходится, называется областью сходимости этого ряда. Ясно, что Х Í Х', где Х' – область определения членов ряда.

Пример 3.8.

Облаcтью сходимости ряда 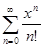является вся действительная прямая (-¥, +¥), поскольку этот ряд сходится абсолютно при любом действительном х (убедиться самостоятельно, применив признак Д'Аламбера). Суммой этого ряда является функция e^x, т.е.

.

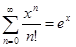Ряд 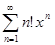сходится только при х = 0; для любого иного действительного х этот ряд расходится. Следовательно, область сходимости ряда вырождается в точку {0}.n

На функциональные ряды нельзя непосредственно перенести свойства конечных сумм действительных функций. Так, конечная сумма непрерывных функций также непрерывна; для функциональных рядов это не так. Рассмотрим последовательность непрерывных на отрезке [0, 1] функций x^n-1×(x-1), n = 1, 2, … и составленный из них функциональный ряд

.

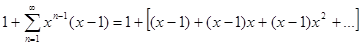Этот ряд сходится в любой точке отрезка [0, 1], причем

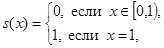
т.е. сумма ряда s(x)является функцией, разрывной в точке х = 1. Для сохранения свойств функций – членов функционального ряда – требуется более сильное условие, чем просто сходимость ряда. Таким условием является равномерная сходимость ряда.

Функциональный ряд 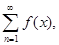сходящийся на Х, х Î Х, сходится на Х равномерно, если для любого e > 0 существует номер N такой, что для всех n > N и всех х Î Х выполняется неравенство

|s_n(x) –s(x)| <e,

где s_n(x) – частичная сумма ряда порядка n, а s(x) – сумма ряда.

Формальная запись: "e $N "n "x n > N Ù хÎ Х Þ |s_n(x) –s(x)| <e

Критерий Коши равномерной сходимости ряда. Для того, чтобы функциональный ряд

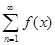, х Î Х

равномерно сходился на множестве Х, необходимо и достаточно, чтобы для любого e > 0 существовал такой номер N, что для всех n > N, целых p ³ 0 и х Î Х выполнялось неравенство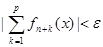

Формальная запись: " e $ N " n " p " x n > N Ù p ³ 0 Ù хÎ Х Þ 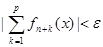n

Признак Вейерштрасса равномерной сходимости ряда. Если для функционального ряда 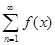, имеющего область сходимости Х, х Î Х, существует числовой сходящийся ряд 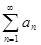такой, что для всех х Î Х

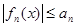, n = 1, 2, …,

то исходный функциональный ряд сходится равномерно и абсолютно на множестве Х.n

Пример 3.9.

Рассмотрим функциональный ряд 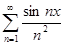. Поскольку

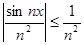, n = 1, 2, …

для всех действительных х, а числовой ряд 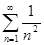сходится, то исходный функциональный ряд сходится абсолютно и равномерно на всей действительной оси - ¥ < х < + ¥n