Числовые ряды

Числовой ряд 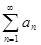называют сходящимся, если последовательность его частичных сумм {s_n} имеет конечный предел 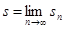, который в этом случае называют суммой ряда и пишут . Если последовательность {s_n} не имеет конечного предела, ряд называют расходящимся.

Критерий Коши сходимости ряда. Числовой ряд 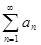сходится тогда и только тогда, когда для любого e > 0 существует такой номер N, что для всех n ³ N и всех целых p ³ 0 выполняется неравенство

Формальная запись: " e $ N " n " p n ³ N Ù p ³ 0 Þ n

Пример 3.2.

Примером сходящегося ряда является сумма членов бесконечной геометрической прогрессии при условии, что |q|<1. В этом случае . Если же |q| ³ 1, то мы получаем пример расходящегося ряда n

Если ряд 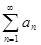сходится, то последовательность его членов {a_n} стремится к нулю, т.е. n

Обратное утверждение неверно: последовательность членов гармонического ряда стремится к нулю, , а сам ряд расходится. n

Если и – два сходящихся ряда и l – действительное число, то сходятся и ряды

, ,

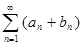причем , а ; эти ряды называются, соответственно, суммой исходных рядов и произведением ряда 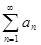на число l. n

Знакочередующимся называется ряд, члены которого попеременно положительны и отрицательны, т.е.

a₁ - a₂ + a₃ - a₄ +¼ +(-1)ⁿ⁺¹ a_n + ¼; a_n >0, n = 1, 2, ….

Признак Лейбница. Если члены знакочередующегося ряда монотонно убывают по абсолютной величине, т.е. a _n+1 < a _n, и стремятся к 0, , то ряд сходится. n

Пример 3.3.

Простейшие примеры сходящихся знакочередующихся рядов:

,

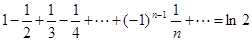n

Важную роль в теории рядов играют ряды с неотрицательными членами, 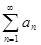, a_n ³ 0, n = 1, 2, ¼.

Для того, чтобы такой ряд сходился, необходимо и достаточно чтобы последовательность его частичных сумм {s_n} была ограничена сверху n

Если же он расходится, то его частичные суммы стремятся к бесконечности, . В этом случае принято использовать обозначение

.

Для рядов с неотрицательными членами ниже приводятся три признака сходимости.

Признак Д'Аламбера. Если для ряда 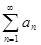существует такое число q,
0 < q < 1, что начиная с некоторого номера выполняется неравенство

,

то данный ряд сходится; если же начиная с некоторого номера

,

то ряд расходится. n

Следствие. Если , то ряд сходится; если , то он расходится. Если , то ряд может как сходиться, так и расходиться; ряды 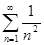и удовлетворяют этому условию, причем первый ряд сходится, а второй – расходится. n

Интегральный признак сходимости. Если для ряда 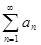с убывающими неотрицательными членами a _n ³ a _n+1 ³ 0, n = 1, 2, ¼ существует функция f(x), определенная и убывающая при х ³ 1, значения которой в целочисленных точках совпадают с членами ряда, т.е. f(n) = a _n, n = 1, 2, ¼, то ряд сходится тогда и только тогда, когда сходится несобственный интеграл

n

Пример 3.4.

Рассмотрим ряд и функцию f(x) = 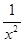. Поскольку

,

то этот ряд сходится. Гармонический ряд расходится, поскольку

n

Признак Коши. Если для ряда 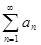существует такое число q, 0 £ q <1, что, начиная с некоторого номера, выполняется неравенство , то этот ряд сходится. Если же, начиная с некоторого номера, имеет место неравенство , то ряд расходится n

Следствие. Если существует и строго меньше 1, то ряд 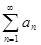сходится; если же этот предел строго больше 1, то ряд расходится n

Пример 3.5.

Ряд сходится, поскольку n

Важность роли рядов с неотрицательными членами следует из свойств абсолютно сходящихся рядов.

Ряд 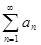называется сходящимся абсолютно, если сходится ряд .

Если ряд абсолютно сходится, то он сходится и в обычном смысле, причем его сумма не зависит от порядка следования слагаемых. n

Сходящийся, но не абсолютно сходящийся ряд называется условно сходящимся.

Сумма условно сходящегося ряда зависит от порядка его членов; по теореме Римана, каково бы ни было число А, можно так переставить члены этого ряда, что сумма получившегося ряда будет равна А. Более того, за счет перестановки членов ряда можно добиться того, чтобы последовательность частичных сумм была бы бесконечно большой, как со знаком «+», так и со знаком «-». n

Пример 3.6.

Ряд , рассмотренный в примере 3.3, является условно сходящимся, ибо гармонический ряд расходится. Если переставить его члены определенным образом, можно изменить значение суммы. Например,

,

где перестановка членов сделана по правилу: за двумя положительными следует один отрицательный, причем порядок положительных членов остается прежним; то же для отрицательных n

Таким образом, для условно сходящихся рядов не имеет места коммутативный закон сложения. Не для всех рядов оказывается справедлив и ассоциативный закон сложения.

Пример 3.7.

Мы рассмотрим расходящийся ряд, который за счет различных группировок его членов можно превратить в сходящийся, причем сумма ряда зависит от способа группировки.

В качестве исходного берем знакопеременный ряд

1 – 1 + 1 – 1 + ¼ + (-1)ⁿ⁺¹ +¼

Для него s₁ = 1, s₂ = 0, s₃ = 1, s₄ = 0 и вообще, s_{2n – 1} = 1,s_2n = 0, n = 1, 2, …, т.е. ряд расходится. При группировке его членов

(1 – 1) + (1 – 1) + …

получаем сходящийся ряд с суммой, равной 0, а при группировке

1 - (1 - 1) - (1 - 1) -…

получаем также сходящийся ряд, но с суммой, равной 1n