Определенный интеграл

Мы рассмотрим наиболее распространенный вариант определенного интеграла – интеграл Римана.

Интегральная сумма заданной действительной функции f(x) на отрезке [a, b], a < b. Зададим произвольное разбиение t отрезка [a, b] на конечное число частей с помощью точек t = { x _i} (i =0, 1, …, n) таких, что a = x₀ < x₁ <... < x_i-1 < x_i <... < x_n = b. Мелкостью разбиения t назовем число l(t) = В каждом промежутке [x_i-1, x_i] разбиения t выберем ровно по одной точке x_i,

x_i-1 £ x_i £ x_i.

Интегральной суммой функции f(x) для разбиения t называется выражение s (t), определяемое как:

.

Ясно, что s(t) зависит от выбора точек (i =1, …, n). Будем рассматривать разбиения t отрезка [a, b] при условии, что мелкость этих разбиений стремится к нулю, т.е. l(t) ® 0; в остальном эти разбиения произвольны. Для этих произвольных разбиений будем подсчитывать интегральные суммы s(t), произвольным образом выбирая точки (i =1, …, n). Заметим, что при l(t) ® 0 число n с необходимостью становится как угодно большим, т.е. n ® ¥.

Число I называется пределом интегральных сумм при l(t) ® 0,

,

если для любого e > 0 найдется такое число d > 0, что для всех интегральных сумм, рассчитанных при мелкости соответствующих разбиений, не превышающих d, т.е. при l(t) < d, выполняется условие |I - s(t)| < e.

Если существует конечный предел I интегральных сумм при мелкости разбиений l(t) ® 0, то функцию f(х) называют интегрируемой по Риману на отрезке [a, b], а < b, а предел I – определенным интегралом Римана от функции f(x) по отрезку [a, b] и обозначают

.

Число а называют нижним пределом интегрирования, число b – верхним пределом, функцию f(х) – подынтегральной функцией, x – переменной интегрирования.

Достаточным условием существования интеграла Римана для функции f(x) по отрезку [a, b] является ее ограниченность и существование не более чем конечного числа разрывов этой функции на отрезке [a, b]. Очевидно, что интеграл Римана существует для непрерывной и кусочно-непрерывной функции на любом отрезке.n

Если a = b, то по определению полагают, что , а если a > b, то по определению,

Отметим, что для любой четной функции, т.е. когда f(x) = f(-x),

(убедиться самостоятельно!),

а для нечетной функции, т.е. когда f(x) = - f(-x),

.

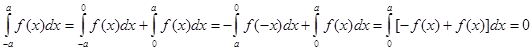Интеграл Римана обладает свойством линейности: если функции f₁(x) и f₂(x) интегрируемы на [a, b], то для произвольных действительных чисел l₁ и l₂ функция l₁ × f₁(x) + l₂ × f₂(x) также интегрируема на этом отрезке и

.n

Справедливо также свойство аддитивности интеграла относительно отрезков, по которым происходит интегрирование: если a < c < b и функция f(x) интегрируема на отрезках [a, c] и [c, b], то она интегрируема и на отрезке [a, b], причем

.

Верно и обратное: из интегрируемости на отрезке [a, b] следует интегрируемость на любом отрезке [c, d], [c, d] Ì [а, b].n

Если функции f(x) и g(x) интегрируемы, то их произведение также интегрируемо. Если f(x) ³ g(x) на[a, b], то

.n

Если функция f(x) интегрируема на [a, b], то ее абсолютная величина | f(x) |также интегрируема на [a, b] и

.n

Интеграл с переменным верхним пределом позволяет установить связь между неопределенными и определенными интегралами.

Если функция f(x) интегрируема по Риману на отрезке [a, b], то функция

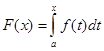, a £ x £ b,

непрерывна на этом отрезке. Если, кроме того, функция f(x) непрерывна в точке x₀ отрезка[a, b], то функция F(x) дифференцируема в этой точке и F'(x₀) = f(x₀). Следовательно, если функция f(x) непрерывна на отрезке [a, b], то функция

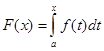
является ее первообразной на этом отрезке, и верна формула

.n

Формула Ньютона-Лейбница. Для любой первообразной F(x) непрерывной функции f(x) на отрезке [a, b] справедлива формула

.

Разность значений одной и той же функции F(b) –F(a) принято обозначать F(x) .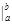

Таким образом, интеграл Римана по некоторому отрезку от непрерывной функции равен разности на концах этого отрезка любой из ее первообразных.

Формула замены переменной. Предположим, что функция f(x) непрерывна на отрезке [a, b], а функция x º j (t) непрерывна вместе со своей производной j' (t) на отрезке [a, b], причем отрезок [a, b] отображается функцией j на отрезок [a, b], так что j(a) = a и j(b) = b. Тогда на отрезке [a, b] имеет смысл суперпозиция f[ j (t)] и справедлива формула

.n

Формула интегрирования по частям. Если функции U(x) и V(x) интегрируемы на отрезке [a, b] вместе со своими производными U'(x) и V'(x), то справедлива формула

.n

Площадь плоской фигуры. Вычисление площадей плоских фигур – это классическая задача, из решения которой и возникло интегральное исчисление.

Для непрерывной функции f(x), f(x) ³ 0 на [a, b], значение интеграла

равно площади криволинейной фигуры, образованной графиком функции f(x), a £ x £ b, отрезком [a, b] оси абсцисс и двумя отрезками прямых x = a и x = b, которые могут вырождаться в точки, как для случая x = b на рис. 2.1.

Если f(x) £ 0 на [b, c], то значение интеграла

равно «отрицательной» площади соответствующей криволинейной фигуры.

В общем случае плоская фигура произвольной формы ограничена графиками двух функций – f₂(x) и f₁(x), f₂(x)³ f₁(x), определенных на отрезке [a, b] как показано на рис. 2.2. Верхняя граница – график функции f₂(x), нижняя граница – график функции f₁(x). В общем случае возможно наличие и боковых границ – отрезков прямых x = a и x = b, которые могут вырождаться в точку, как показано на рисунке. Если на правом конце отрезка [a, b] f₂(b) > f₁(b) и существует боковая граница – отрезок ВС, где Bb = f₂(b), Cb = f₁(b), то левая граница вырождена в точку А, так что Aa = f₂(a) = f₁(a).

Площадь соответствующей фигуры определяется по формуле

.n

Пример 2.4.

Вычислить площадь фигуры, ограниченной линиями

y = |sinx|, y = 0, , .

Эта фигура распадается на две части, левую с площадью S₁ и правую с площадью S₂, т.е. S = S₁ +S₂. Левая часть ограничена сверху графиком функции – sin x, слева – отрезком прямой , снизу – осью абсцисс y = 0, а правая граница вырождена в точку (0,0).

Правая часть ограничена сверху графиком функции sin x, справа – отрезком прямой , снизу – осью абсцисс, а левая граница вырождена в точку (0,0).

Таким образом,

, .

Вычислим эти интервалы по формуле Ньютона – Лейбница.

,

.

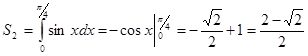Окончательно получаем n

Пример 2.5.

Вычислить площадь фигуры, ограниченной линиями:

y= cos x +1, y = |x|-p/2+1, -p/2 £ x £ p/2.

Эта фигура (рис. 2.4) ограничена сверху косинусоидой y = cos x +1,а снизу - ломаной линией y = |x| - p/2 +1; боковые границы вырождены у нее в точки, (-p/2, 1) и (p/2, 1). Имеем

.

Поскольку подинтегральная функция четная, можно написать

.

Вычисляем интеграл по формуле Ньютона – Лейбница.

.

Окончательно S = 2+ n