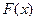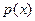|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основные числовые характеристики дискретной случайной величины
|
|
Закон распределения случайной числовой величины характеризует ее полностью, но наиболее компактно можно выразить все существенные сведения о случайной величине, которыми мы располагаем, с помощью числовых параметров, получивших название числовых характеристик случайной величины, из которых рассмотрим математическое ожидание, дисперсию и среднеквадратическое отклонение.
Определение. Математическим ожиданием называется сумма произведений всех возможных значений случайной величины на вероятности этих значений
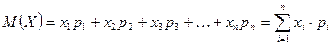 .
.
Математическое ожидание соответствует тому значению случайной величины, около которого группируются все ее возможные значения.
Математическое ожидание обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно этой постоянной величине:
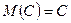 .
.
2. Постоянный множитель 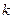 можно выносить за знак математического ожидания:
можно выносить за знак математического ожидания:
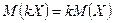 .
.
3. Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий:
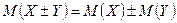 .
.
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
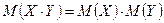 .
.
5. Математическое ожидание отклонения случайной величины от ее математического ожидания всегда равно нулю:
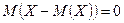 .
.
Пример. Вычислить математическое ожидание дискретной случайной величины  , определяемой как количество посетителей в наугад выбранной аптеке.
, определяемой как количество посетителей в наугад выбранной аптеке.
| Х: | xi | |||||
| pi | 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Решение:
Математическое ожидание дискретной случайной величины Х определяется как сумма произведений всех возможных значений случайной величины на их вероятности:
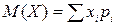 = 5×0,1 +6×0,2 +7×0,3 + 8×0,3 + 9×0,1 = 7,1.
= 5×0,1 +6×0,2 +7×0,3 + 8×0,3 + 9×0,1 = 7,1.
Определение. Математическое ожидание квадрата отклонения случайной величины от ее математического ожидания называется дисперсией случайной величины
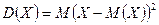 .
.
На практике широко применяется другая формула, значительно упрощающая процесс вычисления
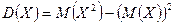 .
.
Дисперсия случайной величины обладает следующими свойствами:
1. Дисперсия постоянной величины 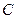 равна нулю:
равна нулю:
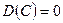 .
.
2. Постоянный множитель 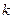 можно выносить за знак дисперсии, предварительно возведя его в квадрат:
можно выносить за знак дисперсии, предварительно возведя его в квадрат:
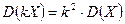 .
.
3. Если  и
и  – независимые случайные величины, то
– независимые случайные величины, то
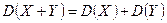 .
.
Пример. Вычислить дисперсию дискретной случайной величины  , используя данные предыдущего примера.
, используя данные предыдущего примера.
Решение:
Дисперсию удобно вычислять по формуле D(X) = M(X 2) – M 2 (X), где
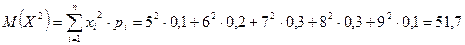 .
.
Таким образом, дисперсия дискретной случайной величины  равна
равна
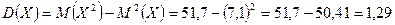 .
.
Дисперсия имеет размерность квадрата размерности случайной величины. Поэтому для оценки рассеяния возможных значений случайной величины вокруг ее математического ожидания ее использовать неудобно. В связи с этим вводят понятие среднего квадратического отклонения, размерность которого совпадает с размерностью случайной величины.
Определение. Корень квадратный из дисперсии называется средним квадратическим отклонением:
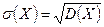 .
.
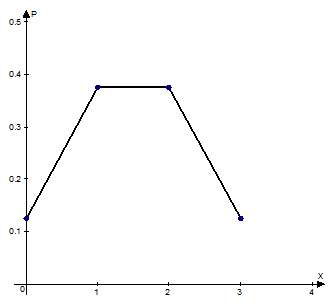
Найти числовые характеристики и построить многоугольник распределения.
Решение.
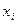
| ||||
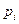
| 0,125 | 0,375 | 0,375 | 0,125 |
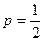 – вероятность рождения девочки
– вероятность рождения девочки
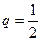 – вероятность рождения мальчика
– вероятность рождения мальчика
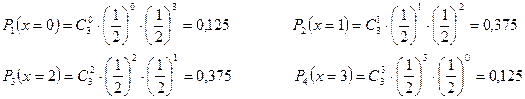
Найдем числовые характеристики:
1. математическое ожидание
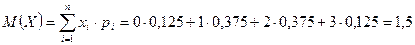
2. дисперсия
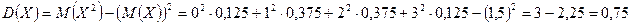 3. среднеквадратическое отклонение
3. среднеквадратическое отклонение
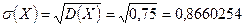
Определение: Функцией распределения НСВ назовем функцию
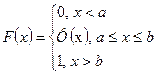
|

Функция 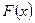 называется интегральной.
называется интегральной.
Определение: Плотностью распределения НСВ назовем функцию 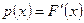
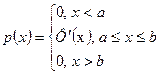
|

Функция 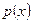 называется дифференциальной.
называется дифференциальной.
Можно выделить основные законы распределения НСВ:
1. нормальное распределение;
2. распределение 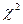 ;
;
3. распределение Стьюдента.
Непрерывные случайные величины обладают следующими характеристиками:
1. математическое ожидание: 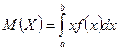
2. дисперсия: 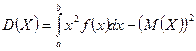
3. среднеквадратическое отклонение: 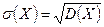
Дата публикования: 2014-10-16; Прочитано: 965 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!