Бесконечно малые и бесконечно большие функции

Определение. Функция называется бесконечно малой (б. м.) при , если

или

Пример. Функция является б.м. при и не является таковой при .

Теорема 1. Пусть — б.м. при , тогда их сумма

также является б.м. при .

Теорема 2. Пусть б. м. при , а 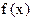ограничена в некоторой окрестности точки а, тогда 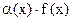является б. м. при .

Пример. Вычислим .

При величина х является б. м., а функция ограничена, так как .

Следовательно, искомый предел, как предел б. м., равен нулю.

Теорема 3. Предел равен числу А в том и только в том случае, когда является б. м. при .

Пример. 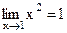означает, что является б. м. при .

Из этого свойства следует, что функцию , имеющую предел А при , можно записать в виде , где есть б. м. при .

Аналогично при .

Основные теоремы о пределах. Пусть 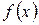и - функции, для которых существуют пределы при (или при ): , . Сформулируем основные теоремы о пределах.

1. Функция не может иметь более одного предела.

2. Предел алгебраической суммы, то тогда существует и равен

А ± В.

3. Если и существуют, то тогда существует и равен .

4. Если и и существуют, то тогда существует и равен .