Основні поняття

Звичайним диференціальним рівнянням називається рівняння вигляду

, ,

що зв'язує незалежну змінну 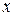, невідому функцію і її похідні .

Порядком диференціального рівняння називається порядок найвищої похідної, такої, що входить до даного рівняння. Наприклад, рівняння першого порядку; другого порядку; третього порядку і т.д.

Розв’язком диференціального рівняння 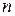-го порядку на інтервалі називається будь-яка функція , що має на цьому інтервалі похідні до 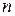-го порядку включно і така, що підстановка функції та ії похідних у диференціальне рівняння перетворює останнє у тотожність коли .

Графік розв’язку диференціального рівняння називається інтегральною кривою цього рівняння.

Задача Коші для рівняння n -го порядку, розв'язане відносно старшої похідної

, (1)

ставиться таким чином. Серед всіх розв’язків рівняння (1) потрібно знайти такий розв’язок, для якого функція разом зі своїми похідними до (n- 1)-го порядку включно приймає задані значення 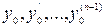при заданому значенні аргументу 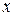,тобто

(2) де задані числа. Умови (2) називаються початковими умовами розв’язку, а сам розв’язок - частинним розв’язком рівняння (1), що задовольняють ці початкові умови (2).

Теорема. Нехай маємо диференціальне рівняння 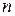-го порядку (1).

Якщо права частина цього рівняння неперервна як функція аргументів в деякому околі точки 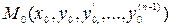, то знайдеться інтервал вісі , на якому існує принаймні один розв’язок рівняння (1), що задовольняє початкові умови

Якщо, крім цього, функція має обмежені частинні похідні 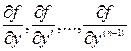у вказаному околі , то такий розв’язок єдиний.

Загальним розв’язком диференціального рівняння n -го порядку (1) в деякому околі існування і єдиності розв’язку задачі Коші називаєтьсяфункція 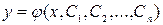, що залежать від 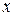та n довільних сталих , така, що

1) за будь-яких допустимих значеннях сталих функція 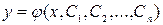є розв’язком диференціального рівняння (1);

2) які б не були початкові умови (2)

(аби точка ) області існування і єдиності розв’язку задачі Коші для рівняння (1)), можна знайти такі значення сталих ,щоб розв’язок задовольняв початкові умови.