 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Укладка графов в трехмерном пространстве
|
|
Определение. Граф G обладает укладкой в некотором пространстве, если он изоморфен некоторому графу  , изображенному в этом пространстве при помощи точек (представляющих вершины
, изображенному в этом пространстве при помощи точек (представляющих вершины  ) и жардановых кривых (представляющих ребра
) и жардановых кривых (представляющих ребра  ), причем никакие 2 кривые нигде не пересекаются друг с другом, кроме инцидентной им обеим вершины.
), причем никакие 2 кривые нигде не пересекаются друг с другом, кроме инцидентной им обеим вершины.
Теорема 1. Каждый конечный граф может быть уложен в трехмерном пространстве.
Доказательство:

Пусть в графе G  вершин. На прямой, перпендикулярной плоскости S, расставляем все p вершин. Пусть множество ребер E состоит из ребер
вершин. На прямой, перпендикулярной плоскости S, расставляем все p вершин. Пусть множество ребер E состоит из ребер  . Через прямую, на которой расставлены все p вершин, проводим q плоскостей, перпендикулярных нашей плоскости S. Затем каждое ребро проводим на отдельной плоскости. Пересечений у этих ребер не будет, кроме вершин. В нашем доказательстве мы предъявили укладку в трехмерном пространстве. Теорема доказана.
. Через прямую, на которой расставлены все p вершин, проводим q плоскостей, перпендикулярных нашей плоскости S. Затем каждое ребро проводим на отдельной плоскости. Пересечений у этих ребер не будет, кроме вершин. В нашем доказательстве мы предъявили укладку в трехмерном пространстве. Теорема доказана.
5.9. Планарность.
Формула Эйлера для плоских графов
Определение. Граф называется плоским, если онуложен на плоскости.
Определение. Граф называется планарным, если он изоморфен некоторому плоскому графу.
Пример: Пусть даны графы G и H, где G – плоский, H – не плоский, но планарный, так как  .
.

Плоский граф разбивает нашу плоскость на области, которые называются гранями. Грани бывают ограниченными и неограниченными. В дальнейшем грани будем обозначать через  , а число граней – через m.
, а число граней – через m.
Пример. Пусть дан граф:

где g1, g2 – ограниченные грани, g3 – неограниченная грань.
Теорема 2 (формула Эйлера). Пусть G – связный плоский граф, у которого p вершин, q ребер и m граней, тогда имеет место соотношение, что
p + m = q + 2. (2)
Доказательство (индукцией по q):
Пусть q=0, тогда граф имеет 1 вершину, т.е. p = 1, m = 1, так как грань только одна – неограниченная. Соотношение (2) справедливо, 1 + 1 = 0+ 2.
Пусть соотношение (2) справедливо для графа, число рёбер которого меньше q.
Теперь докажем справедливость соотношения (2) для графа с q рёбрами.
Рассмотрим произвольное ребро e графа G. Возможны 2 случая:
1)  – петля. Тогда из графа G удалим это ребро e, получим граф, у которого p вершин, q –1 ребер, m –1 граней. Но поскольку по индукционному предположению верна формула Эйлера, то p+m–1 = q–1+2. Прибавив 1 слева и справа, получим нашу формулу: p+m = q+2.
– петля. Тогда из графа G удалим это ребро e, получим граф, у которого p вершин, q –1 ребер, m –1 граней. Но поскольку по индукционному предположению верна формула Эйлера, то p+m–1 = q–1+2. Прибавив 1 слева и справа, получим нашу формулу: p+m = q+2.
2)  , где
, где  . Удаляем ребро e, получаем граф H. Возможны 2 случая:
. Удаляем ребро e, получаем граф H. Возможны 2 случая:
а)

Граф H – связный, значит, мы можем прийти из вершины 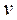 в вершину
в вершину  по другому маршруту. У графа H p вершин, (q–1) ребер и
по другому маршруту. У графа H p вершин, (q–1) ребер и
(m–1) граней, т.е. число граней уменьшается, так как вершины 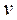 и
и  лежат в разных гранях, а после удаления ребра е грани сливаются. Мы получили случай, аналогичный первому.
лежат в разных гранях, а после удаления ребра е грани сливаются. Мы получили случай, аналогичный первому.
б)
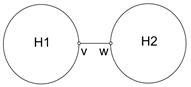
Граф H – несвязный, т.е. после удаления ребра е получаем 2 связные компоненты графа H1, H2: H1 = (p1,q1,m1), H2 = (p2,q2,m2). Для H1 и H2 справедлива формула Эйлера по индукционному предположению p1+m1 = q1+2, p2+m2 = q2+2, p1+p2 = p, q1+q2 = q–1, m1+m2 = m+1, так как вместо одной бесконечной грани стало 2. Сложим наши равенства:
p1+p2+m1+m2 = q1+q2 +4 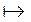 p+m+1 = q–1+4
p+m+1 = q–1+4 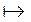 p+m = q+2.
p+m = q+2.
Теорема доказана.
5.10. Следствия из формулы Эйлера
для плоских графов
Следствие 1. Пусть G – связный плоский (p,q,m)-граф без петель и кратных ребер. Тогда q  3p – 6.
3p – 6.
Доказательство. Пусть gi – некоторая грань графа G. Обозначим через  (gi) число ребер, ограничивающих грань gi.
(gi) число ребер, ограничивающих грань gi.  (gi)
(gi)  3, так как нет петель и кратных ребер. Тогда
3, так как нет петель и кратных ребер. Тогда  (m – число граней в графе G), так как каждое ребро ограничивает 2 грани,
(m – число граней в графе G), так как каждое ребро ограничивает 2 грани,  (gi)
(gi)  3. Следовательно, 3m
3. Следовательно, 3m  2q. По формуле Эйлера p+m = q+2, т.е. m = q+2–p, то
2q. По формуле Эйлера p+m = q+2, т.е. m = q+2–p, то
3(q+2–p)  2q
2q 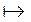 q
q  3p–6.
3p–6.
Следствие 2. Граф K5 не планарен.

Доказательство. Предположим, что граф K5 планарен, тогда существует плоский граф G такой, что 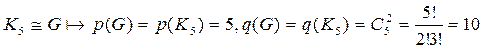 .
.
Так как полный граф без петель и кратных ребер, то по следствию 1  т.е. 10
т.е. 10  3
3  5–6 = 9. Получаем противоречие, значит, граф K5 – не планарен.
5–6 = 9. Получаем противоречие, значит, граф K5 – не планарен.
Следствие 3. Граф K3,3 не планарен.

Доказательство. Пусть граф K3,3 планарен, т.е.  , где G – плоский граф и p(G) = 6, q(G) = 9. Пусть граф G имеет m граней: g1, …,gm.
, где G – плоский граф и p(G) = 6, q(G) = 9. Пусть граф G имеет m граней: g1, …,gm.  – это следует из того, что в графе нет треугольников, т.е. нет цикла из 3 ребер. Значит, из вершины в нее саму мы можем попасть лишь за четное число шагов. Рассмотрим
– это следует из того, что в графе нет треугольников, т.е. нет цикла из 3 ребер. Значит, из вершины в нее саму мы можем попасть лишь за четное число шагов. Рассмотрим  , но
, но 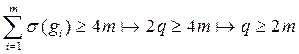 . Но, так как граф G плоский, то справедлива формула Эйлера: p+m = q+2
. Но, так как граф G плоский, то справедлива формула Эйлера: p+m = q+2 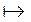 m = q+2–p.
m = q+2–p.
 .
.
Получаем противоречие, значит, граф K3,3 не планарен.
Следствие 4. В любом плоском связном графе G без петель и кратных ребер существует вершина 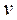 , степень которой не больше 5, т.е.
, степень которой не больше 5, т.е.  .
.
Доказательство. Как известно,  . Предположим, что
. Предположим, что 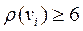 для
для  , где
, где  . Тогда
. Тогда  , т.е.
, т.е.  ,
,  . В силу следствия 1 q
. В силу следствия 1 q  3p–6, пришли к противоречию. Значит, существует вершина
3p–6, пришли к противоречию. Значит, существует вершина 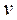 , что
, что  .
.
Дата публикования: 2014-10-20; Прочитано: 3213 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
