Деревья и операции над ними

Введем три операции:

1. Ребро –дерево с корнем (код 01), дереву из одного ребра дается код 01.

2. Если у нас есть дерево с корнем 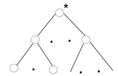, то результат присоединения этого дерева к ребру 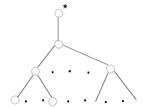–также есть дерево с корнем.

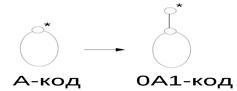
При этом пусть дерево с корнем имеет код А, тогда дереву, полученному в результате операции 2, ставится код 0А1.

3. Если у нас есть два дерева с корнем,

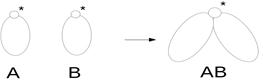
то результат склеивания этих деревьев также есть дерево с корнем. Если при этом у одного дерева код А, а у другого код В, тогда у дерева, которое получается склеиванием этих деревьев, код будет АВ.

Замечание. Любое дерево с корнем можно получить при помощи вышеуказанных трех операций, при этом всегда можно определить его код.

Пример. Пусть дано корневое дерево Т, определить его код, где

Решение: Исходное дерево Т получено из деревьев двукратным применением операции 3, где

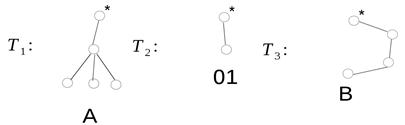
тогда код дерева Т – А01В.

1) Дерево получено из дерева с помощью операции 2, где

,

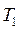
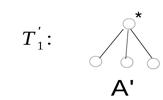тогда код дерева А = 0A'1.

Дерево 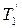получено из дерева операции 1 двукратным применением

операции 3, тогда код дерева 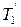A' = 010101, следовательно, код дерева A= 00101011.

2) Дерево Т ₂ получено с помощью операции 1, его код – 01.

3) Дерево Т ₃ получено из дерева операции 1 двукратным применением операции 2, тогда код дерева Т ₃ В = 000111.

В итоге код корневого дерева Т есть код А01В = 0010101101000111.

Свойства кода дерева:

1) Длина кода дерева равна удвоенному числу его ребер (2q).

2) В любом начальном отрезке (если считать код дерева слева) число нулей 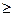числа единиц.

3) Во всем коде число нулей равно числу единиц.

Встает логичный вопрос: как восстанавливать по коду дерево?

Берем произвольный код 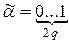дерева, где 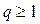, q – число ребер дерева. Идем слева направо и отмечаем такой момент, когда число нулей совпадает с числом 1. При этом возможны два случая:

1) Пусть равенство наступит в конце кода, тогда 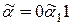, т.е. дерево с кодом 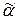получено из дерева с кодом 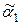с помощью операции 2.

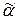2) Пусть равенство наступит, не доходя до конца кода, т.е. , а это означает, что дерево с кодом получено из деревьев соответственно с кодам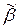и и 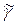с помощью операции 3.

Аналогично, т.е. согласно пунктам 1) и 2), восстанавливаем по кодам 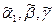соответствующие им деревья. Этот процесс называется декодированием. Не сложно доказать (мы практически уже показали), что между деревом и его кодом существует взаимно однозначное соответствие.

Пример. Построить корневое дерево по его коду .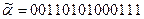

Решение: q = 7. 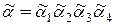, где 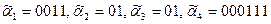. Таким образом, дерево с кодом 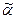получено из деревьев соответственно с кодами 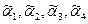с трехкратным применением операции 3. Аналогично, дерево с кодом 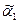получено из дерева операции 1 с применением операции 2; деревья с кодам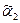и и 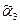– деревья операции 1; дерево с кодом 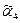получено из дерева операции 1 с двукратным применением операции 2. В итоге дерево Т выглядит следующим образом:

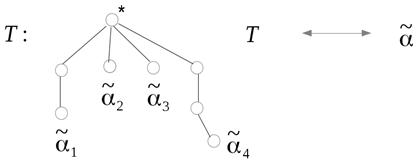
5.16.Оценка числа неизоморфных корневых деревьев
на p вершинах

Обозначим через D(p) множество всех неизоморфных деревьев с корнем на p вершинах.

Лемма 2. Число .

Доказательство. Выше мы показали, что любое дерево можно закодировать набором из 0 и 1 длиной 2q, где q – число ребер дерева, и любому набору из 0 и 1 длиной 2q соответствует дерево с q ребрами. Тогда число всевозможных наборов из 0 и 1 длиной 2q по правилу произведения комбинаторики равно 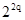. Значит, 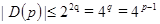, где по свойству 3 дерева p = q + 1. Лемма доказана.

Замечание. Только в одном случае, когда q = 0, p = 1, мы получаем тривиальное дерево.