Элементы теории графов

Начало теории графов можно отнести к 1736 г., когда Л. Эйлер решил задачу о кенигсбергских мостах. В городе Кенигсберге (ныне Калининград) имеются два острова, соединенные семью мостами с берегами реки Преголя и друг с другом. Задача состояла в том, чтобы найти маршрут, проходящий все четыре части города, начинающийся и заканчивающийся в любой из его частей и проходящий ровно один раз по каждому из мостов. Эйлер не только решил эту задачу, но и нашел критерий существования в графе специального маршрута (эйлерова цикла, как теперь его называют). Однако этот результат более ста лет оставался единственным результатом теории графов. Лишь в середине XIX века инженер-электрик Г. Кирхгоф разработал теорию деревьев для исследования электрических цепей, а математик А. Кэли в связи с описанием строения углеводородов решил перечислительные задачи для трех типов деревьев. К этому же периоду относится появление знаменитой проблемы четырех красок.

Родившись при решении головоломок и занимательных игр, теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. В виде графов можно интерпретировать схемы дорог, электрические цепи, географические карты, молекулы химических соединений, связи между людьми и группами людей. В теоретико-графовых терминах формулируется большое число задач, связанных с дискретными объектами. Такие задачи возникают при проектировании интегральных схем и схем управления, при исследовании автоматов, логических цепей, блок-схем программ, в экономике и статистике, химии и биологии, в теории расписаний и дискретной оптимизации. Таким образом, теория графов становится одной из существенных частей математического аппарата кибернетики, языком дискретной математики.

Основные понятия и определения

Определение. Пусть даны 2 множества: V = {v₁,v₂,...} и
E = {(v_i,v_j)/ v_i,v_j 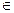V}. Тогда пара (V,E) есть граф, где V – множество вершин, E – множество ребер.

Мы будем рассматривать такие графы, в которых множества V и E конечны, такие графы называются конечными.

Все графы делятся на 2 группы:

1) ориентированные графы или орграфы (когда важен порядок вхождения вершины в пару, которая определяет ребро);

2) неориентированные графы (когда порядок вхождения вершины в пару не важен).

Замечание. По умолчанию граф неориентирован.

Определение. Ребро вида 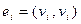называется петлей.

Определение. Ребра вида 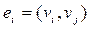, , 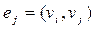где 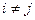, называются кратными.

Определение. Пусть |V| = p, |E| = q, тогда граф, содержащий p вершин и q ребер, называется (p,q)- графом.

Если G – (p,q)-граф, то p(G) – число вершин в графе G, q(G) – число ребер в графе G.

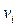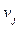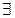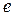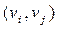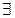Определение. Вершины и называются смежными, если ребро из E вида (если ребро, которое их соединяет). В этом случае также говорят, что вершина 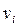и ребро 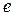инцидентны друг другу.