Деревья и их свойства

Определение. Деревом называется связный граф, который не содержит замкнутых цепей, т.е. нет цикла, в котором ребра разные.

Свойства дерева:

1. В дереве нет петель и кратных ребер.

Доказательство следует из определения дерева, так как петля и кратные рёбра

– замкнутые цепи.

2. Любые 2 вершины v и w соединены единственной цепью.

Доказательство следует из определения дерева.

3. Для дерева справедливо следующее соотношение: p = q + 1 (*), где p – число вершин, q – число ребер.

Доказательство (индукцией по p):

а) p = 1 – дерево состоит из одной вершины, q = 0, тогда соотношение (*) выглядит 1 = 1.

б) Пусть соотношение (*) верно для любых деревьев, у которых вершин меньше, чем p.

в) Рассмотрим дерево с p вершинами. Уберем ребро, соединяющее вершины v и w. Наш граф разбился на 2 подграфа и 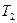. , 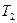– деревья, так как они связны и не имеют замкнутых цепей. Поэтому для них верно индукционное предположение:

V W V W

T ₁ T ₂

.

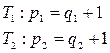
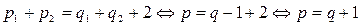4. Если любые 2 вершины v и w в дереве соединить ребром, то получим ровно одну замкнутую цепь.

Доказательство следует из свойства 2.

5. Пусть G = (p, q) – дерево, где p > 1. Тогда в дереве G существуют хотя бы 2 вершины v и w такие, что .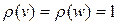

Доказательство. Как известно, 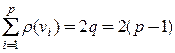(по свойству 3).Предположим, что не существуют 2 вершины, степень которых равна 1, т.е. пусть 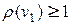, а у остальных вершин 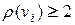, где 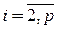. Тогда получаем, что 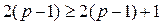. Пришли к противоречию, значит, существуют вершины v и w такие, что .

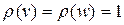Определение. Вершины в дереве, степень которых равна 1, называются концевыми.

Пример дерева:

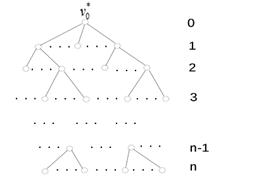
где max(n) – глубина (количество ярусов) дерева, 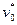– корень дерева (корень – это некоторая выделенная вершина).