Перечисление графов

Определение. Пусть даны графы G и H на одних и тех же занумерованных вершинах 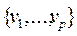. Тогда графы называются равными (G = H), если у них совпадает множество вершин и множество ребер.

Пример:

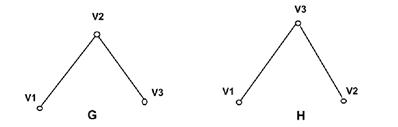
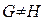, так как в графе G нет ребра 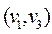, а в графе H это ребро есть, т.е. множества ребер не совпадают.

Поставим 3 задачи и решим их с помощью аппарата комбинаторики. Заметим, что каждому графу соответствует матрица смежности и наоборот.

Задача 1. Сколько всего графов без петель и кратных ребер с p вершинами?

Решение: Построим матрицу смежности, она выглядит следующим образом:

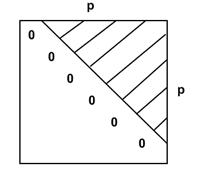
Для решения задачи надо подсчитать число всевозможных вариантов в заштрихованной области. Заштрихованная область имеет 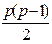позиций. Тогда графов будет 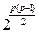, так как в каждой позиции может быть 0 или 1.

Задача 2. Сколько 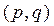-графов без петель и кратных ребер?

Решение: На главной диагонали матрицы смежности стоят одни 0, так как граф без петель. Матрица состоит из 0 и 1, так как граф без кратных ребер. Матрица симметричная, так как граф неориентирован. Число 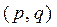-графов – это число способов расстановки в заштрихованной области q единиц, т.е. .

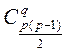Задача 3. Сколько 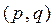-графов без петель, но с кратными ребрами?

Решение: Матрица симметричная, на главной диагонали нули, состоит из чисел множества {0,1,…,q} (т.е. каждая позиция матрицы занята числом из множества {0,1,…,q}).

Число 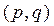-графов без петель, но с кратными ребрами, – это число способов расстановки с повторениями q чисел на местах 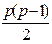, т.е. 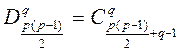(q – сочетание с повторениями из ).

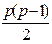Определение. Графы G и H называются изоморфными 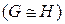, если существует взаимно однозначное соответствие между их вершинами и ребрами такое, что соответствующие ребра соединяют соответствующие вершины, в противном случае графы G и H называются неизоморфными .

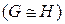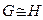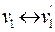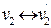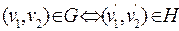Замечание. По другому (изоморфны), если существует взаимно однозначное соответствие между множествами их вершин, которое сохраняет смежность, т.е. если , , то , где , .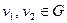

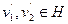Пример:

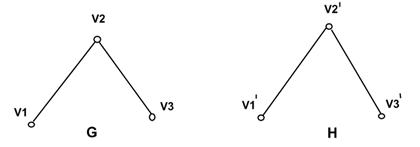а)

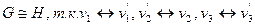, и это соответствие сохраняет смежность.

б)

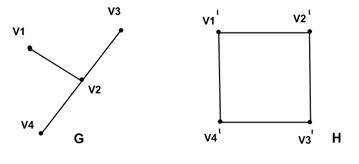
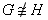, так как смежность не сохраняется.

в)

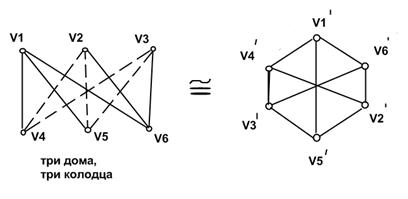
5.6. Оценка числа неизоморфных графов
с p вершинами

Пусть 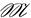(p) – множество графов из p вершин, 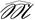(p) – множество всех неизоморфных графов из 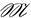(p) (разных с точностью до изоморфизма). Очевидно, что | 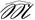(p)|≤ | 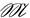(p)|, где 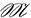(p) и 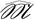(p) – конечны.

Берем любой граф G 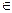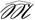(p), тогда устраивая перенумерование p вершин, можно получить p! других вершин. Значит, из каждого графа G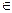 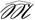(p) можно получить не более p! графов. А поскольку каждый граф из 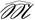(p) получается переработкой, то

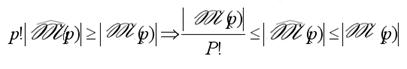
(1)

Соотношение (1) дает оценку числа неизоморфных графов с
р вершинами.