Некоторые соотношения в графе

Определение. Пусть , тогда – число ребер, инцидентных вершине (число называют степенью вершины).

Замечание. В примере 1 (с. 78) . Если 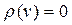, то вершина 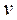изолирована.

Утверждение. Пусть 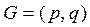– граф без петель. Тогда .

Доказательство очевидное. Каждое ребро дает в сумму вклад 2, так как оно учитывается 2 раза.

Определение. Пусть G – граф без петель и кратных ребер. Тогда он называется полным, если любые две его вершины смежны. Полный граф обозначим через K_p, где p – число его вершин.

Замечание. Совершенно очевидно, что в полном графе число его ребер

.

Пример:

K4: K5: K3:

, ,

Определение. Пусть дан граф , тогда называется подграфом графа , если и .

Определение. Маршрутом в графе G называется последовательность ребер вида: ;

цепью – такой маршрут, в котором все ребра различны;

циклом – замкнутый маршрут.

В примере 1

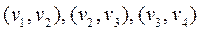– маршрут и цепь;

– цикл.

Определение. Граф называется связным, если для любых двух его вершин существует маршрут, который их соединяет, т.е. . В противном случае граф называется
несвязным.

Замечание. Так как мы имеем дело с конечными графами, то любой граф можно представить в виде конечного объединения связных подграфов. Такие подграфы называются компонентами связности.