Оценка числа неизоморфных графов с q ребрами

Пусть γ(q) – число неизоморфных графов без изолированных вершин с q ребрами.

Лемма 1. 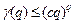, где с – некоторая константа.

Доказательство: Так как по условию существует q ребер, значит различных концов в графе не более 2q, значит, в нашем графе не более 2q вершин. Эти вершины занумеруем числами:

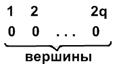
Начало графа можно выбрать 2q способами, конец – тоже 2q способами. Значит, всего возможностей разместить q ребер будет 2q*2q =4q². Таким образом наша задача нахождения числа неизоморфных графов γ(q) сводится к нахождению числа сочетаний с повторениями из 4q² позиций по q. Это число

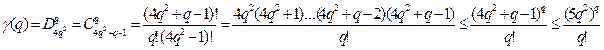
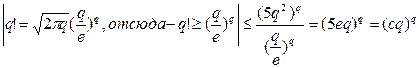= , где с =5e.

Лемма доказана.