 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Полные системы. Теорема 4. Каждая булева функция может быть реализована формулой над множеством
|
|
Теорема 4. Каждая булева функция может быть реализована формулой над множеством  .
.
Доказательство: Рассмотрим 2 случая для функции 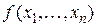 :
:
1) 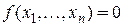 , тогда мы можем представить
, тогда мы можем представить  по пункту 3 теоремы 2.
по пункту 3 теоремы 2.
2)  , тогда из следствия 1 теоремы 3 следует, что
, тогда из следствия 1 теоремы 3 следует, что 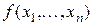
 .
.
Определение. Система функций 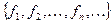 из
из  называется полной в
называется полной в  , если любая булева функция может быть записана в виде формулы над этой системой.
, если любая булева функция может быть записана в виде формулы над этой системой.
Замечание. Из теоремы 4 следует, что система  полна в
полна в  .
.
Следующая теорема позволяет сводить вопрос о полноте одних систем к вопросу о полноте других систем.
Теорема 5. Пусть даны две системы функций из  :
:
 , (I)
, (I)
 , (II)
, (II)
относительно которых известно, что система I полна в  и каждая её функция выражается в виде формулы через функции системы II. Тогда система II является полной в
и каждая её функция выражается в виде формулы через функции системы II. Тогда система II является полной в  .
.
Доказательство: Пусть  – произвольная функция из
– произвольная функция из  . В силу полноты системы I можно выразить
. В силу полноты системы I можно выразить  формулой над
формулой над  , то есть
, то есть
 .
.
По условию теоремы:
 ,
,
 ,
,
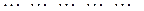
Тогда  .
.
То есть мы выразили произвольную функцию  в виде формулы над множеством
в виде формулы над множеством  , значит, система II полна в
, значит, система II полна в 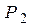 .
.
Дата публикования: 2014-10-20; Прочитано: 791 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
