 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Разложение булевых функций
|
|
Теорема 2. Каждая функция 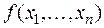 из
из 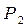 может быть представлена следующим образом:
может быть представлена следующим образом:
1. 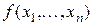
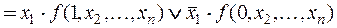 ,
,
2.  ,
,
3.  .
.
Доказательство пункта 1: Возможны два случая:
1)  , тогда
, тогда  .
.
2)  , тогда
, тогда 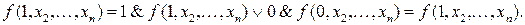
Аналогично доказываются пункты 2 и 3.
Теорема 3. Каждая функция  из
из 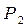 при
при  , представима в виде:
, представима в виде:
1. 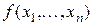
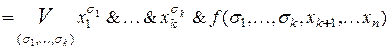 ,
,
где 

2.  , где
, где 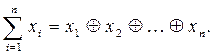
3. 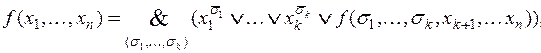 ,
,
где 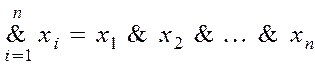 ,
, 
Доказательство пункта 1: Рассмотрим произвольный набор длины  .
.
Слева мы имеем  .
.
Учтем, что


|
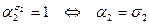


а это означает, что  .
.
Так как  , значит,
, значит,  равна нашей формуле в том и только в том случае, когда
равна нашей формуле в том и только в том случае, когда  .
.
Отсюда 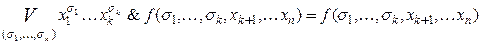 – это справа, так как остальные конъюнкции = 0. А слева мы получаем то же выражение, потому что
– это справа, так как остальные конъюнкции = 0. А слева мы получаем то же выражение, потому что  . Итак,
. Итак,  .
.
Пункты 2 и 3 доказываются аналогично.
Дата публикования: 2014-10-20; Прочитано: 788 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
