Алгебра множеств

Операции над множествами обладают свойствами, которые отчасти напоминают свойства действий над числами, а отчасти отличны от этих свойств.

1. Для любых множеств Х и Y выполняются равенства

а) Х U Y = Y U X;

б) Х ∩ Y = Y ∩ X

(аналог тождеств х+y = y+x и хy = ух).

2. Для любых трех множеств Х, У, Z выполняются равенства

а) (Х U Y)U Z = Х U (Y U Z);

б) (Х ∩Y) ∩ Z = Х ∩ (Y ∩Z)

(аналог тождеств (х+y) +z = х+ (y+z)и (хy) z = х (уz));

в) (Х U Y) ∩ Z = (Х ∩Z)U(Y ∩Z)

(аналог тождества (х+y) z = хz+уz);

г) (Х ∩Y)U Z = (Х U Z) ∩ (Y U Z)

(аналога в обычной алгебре нет).

Пусть все рассматриваемые множества являются частями одного и того же универсального множества U. Дополнение множества Х в множестве U обозначим Х΄, опуская индекс U.

3. Для любого множества Х 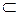U имеет место равенство (Х΄)΄= Х.

4. Выполняются равенства Ø ΄ = U, U΄ = Ø.

5. Для любых двух множеств Х и Y из U имеем:

а) (Х ∩ Y)΄ = Х΄ U Y΄;

б) (Х U Y)΄ = Х΄ ∩ Y΄.

Отметим, что если Х 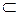Y, то Х ∩Y= Х, Х U Y= Y.

Всегда верны равенства

Ø ∩ Х = Ø,

Ø U Х = Х,

Х ∩ Х = Х,

Х U Х = Х.