Множества и операции над ними

Введём понятие множества с элементами любой природы. Это понятие не определяется, а лишь иллюстрируется примерами. Например, можно говорить о множестве яблок в мешке, множестве квадратов на плоскости, множестве натуральных чисел и т.д.

Множество считается заданным, если о каждом элементе можно однозначно сказать, принадлежит он этому множеству или нет.

В дальнейшем множества обозначим прописными латинскими буквами, а их элементы – строчными буквами. Если элемент x принадлежит множеству X, то пишут x 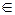X, в противном случае пишут x 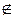X.

Пример 1. Если X – множество русских слов из словаря В.И. Даля, то «семья» 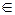X, а 8 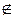X.

Пример 2. Если N – множество натуральных чисел, то 4 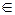N, а 0,3 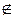N.

Два множества называются равными, если они состоят из одних и тех же элементов. Например, множество равносторонних треугольников равно множеству равноугольных треугольников, а множество параллелограммов – множеству четырехугольников, имеющих центр симметрии. Если множества Х и Y равны, то пишут Х = Y.

Множество, не содержащее ни одного элемента, называют пустым множеством. Его обозначают Ø.

Множества бывают конечными и бесконечными. Множество яблок в мешке, рыб в океане, видов живых существ конечны – количество их элементов можно выразить натуральным числом (хотя мы не всегда знаем значение этого числа). Множества натуральных чисел, ромбов на плоскости, шаров в пространстве бесконечны. Конечное множество можно задать списком его элементов. Два списка элементов одного и того же множества Х могут отличаться друг от друга лишь порядком элементов. Например, {1,2,3} и {2,3,1} – списки одного и того же множества {1,2,3} = {2,3,1}.

В дальнейшем мы будем обозначать число элементов конечного множества Х через | X | и называть это число мощностью множествa Х. МножествоX, содержащее n элементов, будем называть n – элементным множеством, где | X | = n.

Пример 3. Пусть Х – множество простых чисел, меньших, чем 20, т.е. Х= {2,3,5,7,11,13,17,19}. | X | =8.

Бесконечное множество списком задать нельзя. Его задают обычно характеристическим свойством, т.е. свойством, которым обладают все элементы множества и не обладают элементы, не принадлежащие этому множеству.

Множество, заданное характеристическим свойством Р(х), обозначают {х | Р(х)}. Например,запись {х | х² -7х+ 12= 0} обозначает множество корней уравнения х² -7х+12= 0, т.е. множество {3,4}.

Если каждый элемент множества Х является в то же время элементом множества Y, то говорят, что Х – подмножество множества Y. В этом случае пишут: Х 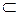Y. Например, множество квадратов является подмножеством множества ромбов, а множество ромбов – подмножеством множества параллелограммов. Множество натуральных чисел, делящихся на 10, является подмножеством множества четных натуральных чисел.

Очевидно, что

1) если Х 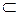Y и Y 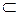Z,то Х 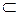Z;

2) если Х 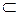Y и Y 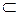X, то Х = Y;

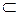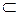3) Ø Х и Х X.

Определение. Пересечением множеств Х и Y называется множество Х ∩Y, состоящее из элементов, которые принадлежат как X, так и Y.

Например, множество квадратов является пересечением множества прямоугольников с множеством ромбов.

Определение. Объединением множеств Х и Y называется множество Х U Y, состоящее из элементов, которые принадлежат хотя бы одному из множеств Х,Y.

Например, множество треугольников является объединением множеств косоугольных и прямоугольных треугольников.

Аналогично определяются операции пересечения и объединения над юбыми совокупностями множеств. Определение. Разностью множеств Х иается множество
Х \ Y, состоящее из всех элементов множества Х, не принадлежащих множеству Y. Если Y 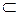Х, то разность Х \ Y = Y΄_x называют дополнением множества Y в множестве X (т.е. Х = Y U Y΄_x).

Например, разностью множества четных чисел и множества чисел, кратных 3, является множество четных чисел, не делящихся на 6. Дополнением множества квадратов в множестве прямоугольников является множество прямоугольников с неравными соседними сторонами.

Изобразим схематически операции над множествами Х и Y:

Такие изображения множеств и операций над ними называют диаграммами Эйлера-Венна.