ББК 22.174 я73

ЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

© Михеева Е. А., 2013

© Ульяновский государственный университет, 2013

Оглавление

Введение...................................................................................................... 6

Раздел 1. Элементы теории множеств..................................................... 8

1.1. Множества и операции над ними................................................... 8

1.2. Алгебра множеств......................................................................... 10

1.3. Разбиение множества на подмножества....................................... 11

1.4. Кортежи и декартово произведение множеств............................ 12

1.5. Отображение множеств................................................................. 13

1.6. Отношения..................................................................................... 14

1.7. Свойства бинарных отношений.................................................... 14

1.8. Алгебра подмножеств................................................................... 15

1.9. Задания для самостоятельной работы......................................... 15

Раздел 2. Элементы комбинаторики..................................................... 20

2.1. Комбинаторика............................................................................. 20

2.2. Различные комбинаторные соотношения.................................... 20

2.3. Свойства биномиальных коэффициентов.
Биномиальная теорема. Полиномиальная теорема...................... 23

2.4. Принцип включения и исключения.............................................. 27

2.5. Формула решета........................................................................... 28

2.6. Производящие функции................................................................ 29

2.7. Производящие функции числа основных комбинаторных
объектов.......................................................................................... 32

2.8. Задания для самостоятельной работы......................................... 34

Раздел 3. Алгебра логики....................................................................... 36

3.1. Булевы функции............................................................................ 36

3.2. Формулы....................................................................................... 39

3.3. Сопоставление формулам над множеством В функций.............. 40

3.4. Свойства элементарных функций................................................. 41

3.5. Разложение булевых функций...................................................... 42

3.6. Совершенная д.н.ф., совершенная к.н.ф...................................... 44

3.7. Полные системы............................................................................ 44

3.8. Примеры полных систем.............................................................. 46

3.9. Полиномы Жегалкина................................................................... 46

3.10. Единственность представления булевых функций
полиномами Жегалкина................................................................. 47

3.11. Методы построения полиномов................................................. 48

3.12. Замыкание. Свойства операции замыкания. Замкнутые классы 50

3.13. Классы 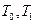и их свойства.......................................................... 51

3.14. Линейные функции и их свойства............................................... 52

3.15. Принцип двойственности............................................................ 53

3.16. Самодвойственные функции, их свойства.................................. 54

3.17. Лемма о несамодвойственной функции...................................... 55

3.18. Монотонные функции, их свойства............................................ 56

3.19. Лемма о немонотонной функции................................................ 57

3.20. Теорема о полноте в 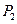............................................................... 57

3.21. Предполные классы.................................................................... 59

3.22. Возможность выделить из любой полной системы
полную подсистему, состоящую из не более чем 4-х функций.... 59

3.23. Представление о результатах Поста.......................................... 60

3.24. Задания для самостоятельной работы....................................... 61

Раздел 4. Синтез управляющих систем................................................. 62

4.1. Схемы из функциональных элементов......................................... 62

4.2. Определение схем из функциональных элементов...................... 63

4.3. Основные понятия и определения................................................ 64

4.4. Возможность реализации любой функции алгебры логики СФЭ 66

4.5. Простейшие методы синтеза......................................................... 69

4.6. Метод Шеннона............................................................................. 71

4.7. Асимптотически наилучший метод (метод О. Б. Лупанова)....... 72

4.8. Задания для самостоятельной работы......................................... 75

Раздел 5. Теория графов......................................................................... 77

5.1. Элементы теории графов.............................................................. 77

5.2. Основные понятия и определения................................................ 78

5.3. Способы задания графа................................................................ 78

5.4. Некоторые соотношения в графе................................................. 80

5.5. Перечисление графов.................................................................... 81

5.6. Оценка числа неизоморфных графов с р вершинами................. 84

5.7. Оценка числа неизоморфных графов с q ребрами...................... 84

5.8. Укладки графов. Укладка графов в трехмерном пространстве. 85

5.9. Планарность. Формула Эйлера для плоских графов................. 86

5.10. Следствия из формулы Эйлера для плоских графов................ 88

5.11. Операция подразделения ребра................................................. 89

5.12. Гомеоморфность графов............................................................. 90

5.13 Теорема Понтрягина-Куратовского............................................ 90

5.14. Деревья и их свойства................................................................. 91

5.15. Деревья и операции над ними.................................................... 92

5.16. Оценка числа неизоморфных корневых деревьев
на р вершинах................................................................................ 95

5.17. Задания для самостоятельной работы....................................... 96

Литература............................................................................................. 100