П.2. Графо-аналитический метод для решения игры с двустолбцовой матрицей выигрышей

применяется, если цена игры .

Метод основывается на равенстве (2.1). Поскольку обоснование этого метода базируется на положениях, близких к положениям, изложенным в предыдущем пункте. Поэтому метод излагаться будет несколько менее подробно, чем метод для двустрочной матрицы.

Если в (2.1) взять по минимум от обеих частей равенства, то цену игры получим из равенства

. (2.20)

Обозначим

, (2.21)

, (2.22)

. (2.23)

Пусть , т.е. в силу (2.22) и (2.23) . Отсюда для всех . Тогда в силу (2.21)

. (2.24)

Так как – цена игры, то согласно теореме 2.2.1 (оптимальности) 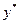является оптимальной смешанной стратегией второго игрока.

Для вычисления и 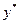проведем следующие графические построения. Пусть – произвольная смешанная стратегия второго игрока. Обозначим . Тогда . Учитывая это и (2.21)–(2.23) введем следующие функции одномерного аргумента :

,

.

Тогда

,

а вместо нахождения точки 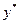минимума функции следует найти точку минимума функции .

Пусть, например, . На рис. 3 изобразим графики функций и темной линией – график функции . Рис. 3 показывает, что точка является решением уравнения , а .

Рис.3

Таким образом, на первом этапе решения игровой задачи с двустолбцовой матрицей находятся цена и оптимальная стратегия 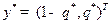второго игрока.

В случаях матрица имеет седловую точку, которая и является решением.

Пусть теперь , т.е. . Тогда по теореме 2.2.2 о дополняющей нежесткости

(2.25)

Обозначим

.

Если , то . Тогда по теореме о дополняющей нежесткости . Поэтому в системе (2.25) для каждого полагается . Если после этого в системе остаются две неизвестных, то ее решением завершается отыскание оптимальной стратегии первого игрока. Исследуем случай, когда в множестве остаются более двух индексов, т.е. в системе (2.25) остаются более двух неизвестных. Выберем любые три индекса . Пусть – соответствующие этим индексам строки матрицы . Так как эти три вектора двумерные, а число их больше двух, они линейно зависимы. Значит, найдутся такие числа не все равные нулю, что будет выполнено равенство

. (2.26)

Умножая его скалярно на оптимальную стратегию второго игрока, получим

. (2.27)

Так как , то

. (2.28)

Подставляя (2.28) в (2.27) и учитывая, что , получим

. (2.29)

Таким образом, среди есть числа разных знаков. Пусть, например . Представим тогда равенство (2.29) в виде

(2.30)

Из (2.26) следует

.

Так как в этом равенстве коэффициенты неотрицательны и для них выполняется соотношение (2.30), то вектор является выпуклой комбинацией векторов . Следовательно, по определению 1.2 -ая чистая стратегия первого игрока является минорирующей. Согласно теореме 1.2 существует оптимальная смешанная стратегия первого игрока с . Тогда в системе (2.25) полагаем . Проделывая такую операцию с каждой тройкой векторов-строк матрицы , оставим в системе (2.25) две неизвестных величины, которые и найдем, решая эту систему.

Пример 2.2. Определить цену и оптимальные стратегии игроков в матричной игре с

.

Решение. Построим 6 функций

и функцию 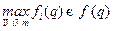. Последняя функция на рис.4 выделена темной линией.

Рис.4

Согласно рис.4 точка является решением, например, уравнения . Решая это уравнение, найдем . Тогда , а . Множеством активных индексов является . Тогда . Минорирующими стратегиями первого игрока будут первая и пятая (на рис.4 графики функций лежат между графиками функций ). Поэтому существует оптимальная стратегия первого игрока, для которой . Таким образом, система (2.19) для данного примера имеет вид

Решая эту систему, находим Итак, задача решена. Ответ: , , .