Столбцы, – строки матрицы А. Столбец и к-ая чистая стратегия второго игрока называются мажорирующими, если найдутся такие числа

, (1.2)

что

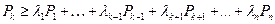, (1.3)

и называется строго мажорирующими, если неравенство (1.3) выполняется как строгое.

Вектор и к-ая чистая стратегия второго игрока называются минорирующими, и строго минорирующими, если в (1.3) выполняются, соответственно, неравенства и <. Аналогичная терминология используется и для строк и чистых стратегий первого игрока.

Теорема 1.1 (о мажорирующей стратегии второго игрока). Пусть игра Г определена матрицей (1.1), а игра – матрицей

;

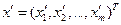– цена, , – оптимальные смешанные стратегии первого и второго игроков в игре .

Если столбец матрицы является мажорирующим, то число

V = является ценой, вектор и вектор , для которого , при j=1, …, к-1, к+1,…, n, являются оптимальными смешанными стратегиями первого и второго игроков в игре Г. При этом, если столбец является строго мажорирующим, то в любой оптимальной стратегии второго игрока.

Доказательство. Для оптимальных стратегий , игры согласно теореме 2.2.1 об оптимальных смешанных стратегиях выполняются неравенства

i=1,…, m, (1.4)

j=1,…, k-1, k+1,…, n. (1.5)

Построимвектор , где при j=1, …, к-1, к+1,…, n, т.е. расширение вектора на i- ом месте. Так как к- ая координата вектора равна нулю, то, из (1.4) получим

, i = 1,…, m. (1.6)

Покажем, что неравенство (1.5) выполняется и для индекса j = k. В силу неравенства (1.3) для любого выполняются неравенства

, (1.7)

где коэффициенты удовлетворяют условиям (1.2). Умножим (1.7) на

и просуммируем по i. Тогда, используя неравенство (1.5) и учитывая условия (1.2), получим

. (1.8)

Таким образом, из (1.6), (1.5) и (1.8) следуют неравенства

i=1,…, m, j=1,…, n,

которые в силу следствия теоремы 2.2.1 о необходимых и достаточных условиях оптимальности стратегий доказывают, что стратегии являются оптимальными в игре Г, а число – ее ценой.Первое утверждение теоремы доказано.

Убедимся в справедливости второго утверждения теоремы. Если к- ая чистая стратегия является строго мажорирующей, то неравенства (1.7), а следовательно, и неравенство (1.8) выполняются как строгие. Тогда по теореме 2.2.2 о дополняющей нежесткости во всех оптимальных стратегиях второго игрока. Теорема доказана.

Аналогично доказывается и следующая

Теорема 1.2. (о минорирующих стратегиях первого игрока). Пусть Г – игра с матрицей А, у которой строка является минорирующей, т.е.

, (1.9)

где коэффициенты удовлетворяют условию

; (1.10)

матрица 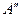получена из матрицы А вычеркиванием ее к – ой строки и – игра, определенная матрицей 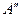. Если – соответственно, цена, оптимальные стратегии первого и второго игроков в игре , то число V= , , а расширение стратегии на к-ом месте, т.е. вектор , являются, соответственно, ценой, оптимальными стратегиями второго и первого игроков в игре Г. Если к – ая чистая стратегия первого игрока в игре Г является строго минорирующей, то в этой игре к – ая координата равна нулю для любой оптимальной стратегии первого игрока.

Доказательство. Пусть , . Тогда в силу теоремы 2.2.1 оптимальностивыполняются неравенства

i=1,…, k-1, k+1,…, n, (1.11)

j=1,…, n. (1.12)

Введем векторы и , где 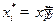при i=1,…, k-1, k+1,…, n. Тогда, распространяя в (1.12) суммирование на все индексы, получим

j=1,…, n. (1.13)

Получим далее неравенство вида (1.11) для i=k. Для этого умножим неравенство (1.9) скалярно на вектор . Учитывая (1.10) и (1.11), получим

. (1.14)

Таким образом, для числа и смешанных стратегий , в силу (1.11), (1.12) и (1.14) выполняются условия

.

Отсюда в силу следствия теоремы 2.2.1 число и смешанные стратегии и являются, соответственно, ценой и оптимальными стратегиями в игре Г. Теорема доказана.

Пример 1.1. Пусть игра определена матрицей

.

Требуется, используя теоремы 1.1 и 1.2, упростить игровую матрицу.

Здесь . Следовательно, третья чистая стратегия второго игрока является мажорирующей. Поэтому существует такая оптимальная стратегия второго игрока, для которой , и третий столбец матрицы можно вычеркнуть. Но поскольку эта стратегия является не строго мажорирующей, то возможно есть и другая оптимальная стратегия второго игрока, в которой третья координата может быть и ненулевой. Замечаем также, что , поэтому в любой оптимальной стратегии второго игрока . Вычеркнем и второй столбец. Итак, вместо решения игры с матрицей А можно находить решение игры с матрицей

.

В матрице вторая строчка стала минорирующей. Поэтому существует оптимальная стратегия первого игрока, в которой . Вторая строка вычеркивается. Остается решить игровую задачу с матрицей

.

В результате решения этой задачи для первого игрока будут найдены первая и третья координаты, а для второго игрока – первая четвертая и пятая координаты их оптимальных стратегий. Остальные координаты равняются нулю.

Как увидим в следующем параграфе игру с двустрочной матрицей можно решить значительно проще, чем методом сведения к задаче линейного программирования.