П.1. Графо-аналитический метод для решения игры с двустрочной матрицей выигрышей

применяется, если цена игры .

Ограничение не является существенным. Подозрение, что цена игры является нулевой, может возникнуть, только если в матрице есть элементы разных знаков. В этом случае можно прибавить одно и то же число С произвольного знака, чтобы все элементы вспомогательной матрицы стали неотрицательными. Решение игры с новой матрицей согласно теореме 2.2.3 о решениях стратегически эквивалентных матричных игр будет совпадать с решением исходной игровой задачи, а для получения цены V нужно будет вычесть число С из найденной цены вспомогательной задачи.

Согласно теореме 2.3.1 матричная игра всегда имеет решение в смешанных стратегиях, т.е. функция выигрыша первого игрока всегда имеет седловую точку, которую обозначим . Тогда по определению цены игры и по теореме 1.4.2 (о седловой точке и максимине) . Отсюда, взяв в обеих частях равенства (2.2) максимум по получим

.

Таким образом, цена V является максимальным значением функции

, (2.6)

которую называют функцией минимума.

Пусть – точка максимума функции (2.6) на множестве смешанных стратегий . Убедимся, что является оптимальной стратегией первого игрока. Действительно, , а для любого выполняются неравенства . Таким образом, для любого . А т.к. V – цена игры, то в силу теоремы 2.2.1 оптимальности смешанная стратегия является оптимальной для первого игрока.

Так как , а точка является смешанной стратегией, то . Обозначим . Тогда .

Обозначим

.

, (2.6)

. (2.7)

Пусть 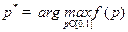. Тогда числа являются координатами оптимальной смешанной стратегии первого игрока.

Лемма 2.1. Если или , то матрица выигрышей имеет седловую точку.

Доказательство. Докажем лемму для случая . Для случая доказательство проводится аналогично.

Так как , а по условию леммы является точкой максимума функции , то согласно (2.7) и (2.6)

.

Таким образом,

(2.8)

Обозначим

.

Убедимся, что найдется такой индекс , для которого . Доказывая это утверждение от противного, предположим, что . Тогда

, , . (2.9)

Если же , то в силу (2.8) . Тогда в силу непрерывности функций 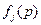найдется такая достаточно близкая к точке точка , что .

Отсюда и из (2.9) для . Но тогда и , тогда как . Полученное противоречие доказывает, что для некоторого индекса выполняется неравенство .

Отсюда и в силу (2.8) выполняются неравенства

, . (2.10)

Условия (2.10) и показывают, что пара индексов является седловой точкой матрицы . Лемма доказана.

Итак, если или , то матрица имеет седловую точку, а она и является решением игры.

Поэтому далее будем считать, что

. (2.11)

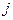Перейдем к разработке алгоритма. Вычислительный процесс основан на графическом построении функций . Эти функции определены для любых значений переменной , но за пределами отрезка [0,1] они не имеют игрового смысла. Обратим внимание на то, что в формуле, определяющей функцию , минимум берется по , а не по . Это значит, что для вычисления значения в точке нужно вычислить числа 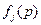, и взять наименьшее из них.

Пусть на рис. 1 , прямые представляют собой графики функци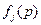й при . Жирной линией изображен график функции . По рис.1 видим, что функция достигает максимума в точке , значение функции в этой точке и является ценой игры 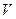. Так как в точке совпадают значения функций , то является решением уравнения . Именно, график позволяет делать такие выводы, поэтому метод и называется графо-аналитическим.

Условие (2.11) означает, что . Следовательно, согласно теореме о дополняющей нежесткости, для оптимальной стратегии второго игрока и цены 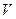, выполняются равенства

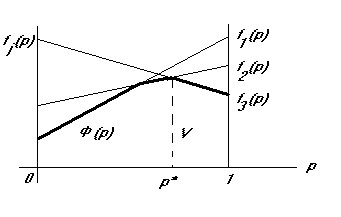
Рис. 1

, (2.12)

.

Обозначим

или в других обозначениях

Если 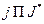, то . Тогда по теореме о дополняющей нежесткости полагаем . В системе (2.12) вычеркиваем слагаемые с индексами 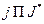. Если после этого в этой системе остается две неизвестных величины , то систему решаем и находим оптимальную стратегию второго игрока.

Исследуем случай, когда после произведенных исключений в системе (2.12) остается более двух неизвестных. Выберем из них любую тройку индексов . Векторы , столбцы матрицы , являются двумерными, а поскольку их число больше двух, то они линейно зависимы. Значит, найдутся такие числа не все равные нулю, что будет выполнено равенство

. (2.13)

Умножая его скалярно на оптимальную стратегию , получим

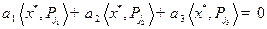. (2.14)

Так как все неизвестные с индексами 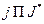были вычеркнуты, то

и, следовательно,

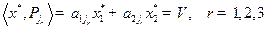. (2.15)

Подставляя (2.15) в (2.14) и учитывая, что , получим

. (2.16)

Таким образом, среди чисел имеются числа разных знаков. Пусть, например . Представим тогда равенство (2.16) в виде

(2.17)

Из (2.13) следует

. (2.18)

В равенстве (2.18) коэффициенты неотрицательны. А т.к. еще выполнено и условие (2.17), то является выпуклой комбинацией векторов . Следовательно, по определению 1.2 -я чистая стратегия второго игрока является мажорирующей. Тогда по теореме 1.1 существует оптимальная смешанная стратегия второго игрока, в которой . В системе (2.12) полагаем . Проделывая такую операцию с каждой тройкой векторов-столбцов в системе (2.12), оставим в ней две неизвестные величины. Решением системы (2.12) двух уравнений с двумя оставшимися неизвестными будет завершен поиск оптимальной стратегии 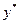второго игрока.

Таким образом, принципиально задача решена, метод построен.

Разберем теперь вычислительный прием, позволяющий легко определить, который из векторов-столбцов матрицы можно удалить, если множество содержит более двух индексов.

Прием 1. Построим на двумерной плоскости координатную систему, построим в ней по координатам векторы для всех . В системе (2.12), оставим только неизвестные, номера которых совпадают с номерами векторов, являющихся крайними для множества построенных векторов.

Прием 2. Пусть установлено, что для тройки индексов выполняется равенство

, (2.19)

где .

Записав (2.19) в координатном виде, получим

Умножив первое из этих равенств на 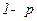, второе на и сложив результаты, получим . В частности, . А это означает, что , где . Значит, на левой вертикальной оси точка лежит между точками . По доказанному ранее правилу и полагается .

Вычислительное замечание. На первом этапе вычислений, т.е. при вычислении оптимальной стратегии первого игрока и цены игры не использовалось условие о том, что цена игры должна быть отлична от нуля. Поэтому на первом этапе можно проводить вычисления, не обращая внимания на условие . Если после первого этапа вычислений окажется, что , то по изложенному алгоритму отыскивается оптимальная стратегия второго игрока. Если же окажется, что , то перед нахождением оптимальной стратегии второго игрока нужно прибавить ко всем элементам матрицы отличное от нуля число и равенства (2.12) выписывать с новыми значениями и продолжать решение. Согласно теореме о эквивалентных матричных играх оптимальные стратегии игроков от такой процедуры не изменяются, а цена игры уже найдена на первом этапе.

Пример 2.1. Требуется найти цену и оптимальные стратегии игроков в игре, определенной матрицей

.

Решение. Выписываем функции

Построим графики этих функций (см. рис.2).

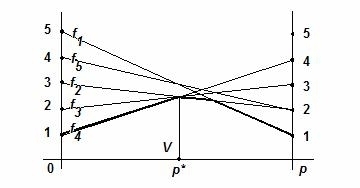
Рис.2

Отметим, что масштабную единицу на оси удобнее брать значительно большей, чем на оси значений функций. Обратим внимание, что все коэффициенты первой строки матрицы (первые коэффициенты функций ) откладываются на первой (правой) вертикальной линии, вторые – на второй вертикальной прямой. На рис.2 график функции выделен жирной линией. По графику видим, что ее максимум достигается в точке , для которой 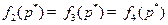. Решим, например, первое из этих равенств . Получим . Значит, координатами оптимальной стратегии первого игрока являются , а цена игры . Поскольку обе координаты оптимальной стратегии первого игрока отличны от нуля, записываем равенства (2.12), которые в данном случае имеют следующий вид:

Так как , . Кроме того, график функции лежит между графиками функций . Поэтому . Таким образом, равенства (2.12) приобрели вид

Решив эту систему, найдем Итак, ответ: цена , оптимальными стратегиями первого и второго игроков являются, соответственно, , .